The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

qad

Summary

The R-package qad (short for quantification of asymmetric dependence) allows to estimate the (directed) dependence of two random variables X and Y. The estimated population value q(X,Y) introduced in [1,3] fulfills the following properties:

• q(X,Y) = 1 if and only if Y is a function of X (knowing X means knowing Y)
• q(X,Y) = 0 if and only if X and Y are independent (no information gain).

While the Pearson correlation coefficient assesses only linear and Spearman rank correlation only monotonic relationships, qad is able to detect any kind of association. For further information we refer to the vignette or the related publications [1,2,3].

Installation

The easiest way to get the package qad is:

install.packages("qad")

In order to install the development version of qad from GitHub:

# install devtools package
if (!requireNamespace("devtools", quietly = TRUE)) {
  install.packages("devtools")
}
# install package
devtools::install_github("griefl/qad", dependencies = TRUE)

Usage

library(qad)

set.seed(314)
n <- 100
x <- rnorm(n)
y <- x^2 + rnorm(n, 0, 1)
plot(x,y, pch = 16)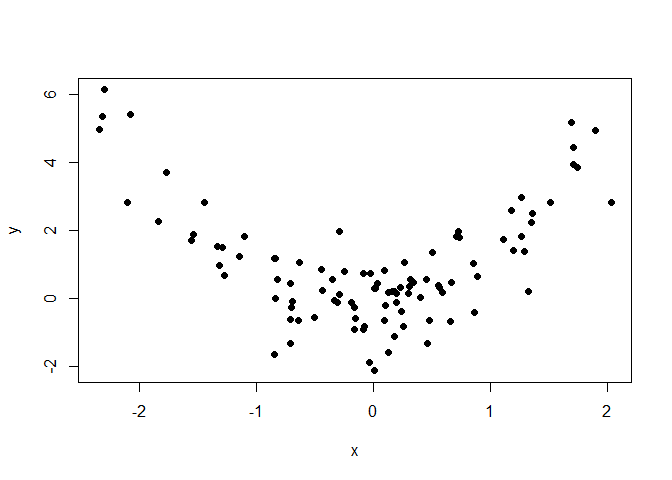

fit <- qad(x,y)
#> 
#> quantification of asymmetric dependence: 
#> 
#> Data: x1 := x
#>       x2 := y
#> 
#> Sample Size: 100
#> Number of unique ranks: x1: 100
#>                         x2: 100
#>                    (x1,x2): 100
#> Resolution: 10 x 10
#> 
#> Dependence measures:
#>                     q p.values
#>  q(x1,x2)       0.610    0.000
#>  q(x2,x1)       0.393    0.002
#>  max.dependence 0.610    0.000
#> 
#>                      a p.values
#>  asymmetry       0.217       NA
coef(fit)
#>         q(x1,x2)         q(x2,x1)   max.dependence        asymmetry 
#>            0.610            0.393            0.610            0.217 
#>       p.q(x1,x2)       p.q(x2,x1) p.max.dependence      p.asymmetry 
#>            0.000            0.002            0.000               NA

#Comparison with correlation
cor(x,y, method = "pearson")
#> [1] -0.04404337
cor(x,y, method = "spearman")
#> [1] 0.06546655
cor(x,y, method = "kendall")
#> [1] 0.05090909

References

• [1] R.R. Junker, F. Griessenberger, W. Trutschnig: Estimating scale-invariant directed dependence of bivariate distributions, Computational Statistics and Data Analysis, (2021), 153, 107058, https://doi.org/10.1016/j.csda.2020.107058

• [2] R.R. Junker, F. Griessenberger, W. Trutschnig: A copula-based measure for quantifying asymmetry in dependence and associations, https://arxiv.org/abs/1902.00203

• [3] W. Trutschnig: On a strong metric on the space of copulas and its induced dependence measure, Journal of Mathematical Analysis and Applications, 2011, (384), 690-705. https://doi.org/10.1016/j.jmaa.2011.06.013

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.