The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

Using motoRneuron for motor unit synchronization

The purpose of this document is to get you started using the motoRneuron package for analyzing motor unit data, even if you’ve never used R before! So we will show you how to install the toolbox through CRAN, access the functions, help files, and sample motor unit data. Next, we will provide code to get typical time series data into a workable format for our functions. Then we will go step-by-step through some analyses with this sample data to demonstrate its applicability.

Time-domain synchronization

It’s assumed that if you’re reading this, you have at least a grasp of what motor unit synchronization means and what you hope to get out of this package. Briefly, time-domain synchronization, in the neuromuscular context we are presenting it, is the tendency of separate motor units (i.e. motor neurons and their associated muscle fibers) to discharge near-simultaneously (within 1 - 5 ms of each other) more often than would be expected by chance. It is often interpreted as an indicator of functional connectivity between motor neurons through common excitatory post-synaptic potentials. This is quanitified by a cross correlation analyses, which is essentially the core of this package. A peak in the resulting cross correlation histogram represents a higher probability of discharges at that latency. Indices that quantify the magnitude of the peak are the primary outputs for the package.

Functions

  1. recurrence_intervals() correlates the discharge times of one motor unit against those of another motor unit.
  2. bin() creates a cross correlation histogram from the recurrence intervals.
  3. plot_bins() plots the cross correlation histogram with ggplot2.
  4. mu_synch() is an all-in-one function that automatically performs the cross correlation process from steps 1 and 2 then assesses the histogram for peaks using 3 optional methods (listed in 4). Six commonly used synchronization indices are returned:
  5. 3 methods of peak determination are available in mu_synch() and as individual functions:
    1. Visual method - visual_mu_synch()
    2. Cumulative Sum (Cumsum) method - cumsum_mu_synch()
    3. Z-score method - zscore_mu_synch()

Package Implementation

Install the package from the Comprehensive R Archive Network or Github and attach it to your workspace with the following functions.

install.packages("motoRneuron")
install.pacakges("devtools")
devtools::install_github("tweedell/motoRneuron")
library(motoRneuron)
library(ggplot2)

View the package or any of the function help files by using ‘?’.

?motoRneuron
?mu_synch

Data: motor_unit_data

Let’s load the sample motor unit data frame from the package into the working environment and look at it before we perform any analyses with it. The data is 30 seconds of 2 concurrently active motor units discharging at semi-regular intervals. It was sampled at 1000 Hz.

motor_unit_data <- motoRneuron::motor_unit_data
head(motor_unit_data)
#>    Time motor_unit_1 motor_unit_2
#> 1 0.000            0            0
#> 2 0.001            0            0
#> 3 0.002            0            0
#> 4 0.003            0            0
#> 5 0.004            0            0
#> 6 0.005            0            0

You’ll see our first column is Time in seconds. The other columns present the activation of “motor unit 1” and “motor unit 2” as a series of binary values. A value of “1” indicates activation of the motor unit at a specific time point, and a value of “0” indicates no activation. Synchronization functions require actual discharge times as inputs… so how is that obtained? We’ll help you out. We included this step because this is a commonly used format for time series data like motor unit discharges. To get the data in a usable form for our functions, we will have to subset out only the time points for which each motor unit has a value of 1.

motor_unit_1 <- data.frame(Time = motor_unit_data[["Time"]], MotorUnit1 = motor_unit_data[[2]])
motor_unit_1 <- subset(motor_unit_1, MotorUnit1 ==1) 
motor_unit_1 <- as.vector(motor_unit_1$Time)
motor_unit_2 <- data.frame(Time = motor_unit_data[["Time"]], MotorUnit2 = motor_unit_data[[3]])
motor_unit_2 <- subset(motor_unit_2, MotorUnit2 ==1)
motor_unit_2 <- as.vector(motor_unit_2$Time)

You’ll see the individual motor unit data is now in vector format containing only the time points of discharge for each motor unit.

head(motor_unit_1)
#> [1] 0.035 0.115 0.183 0.250 0.306 0.377
head(motor_unit_2)
#> [1] 0.100 0.205 0.298 0.377 0.471 0.577

So we’ve got our data in a format that our motoRneuron functions will take.

Calculating recurrence_intervals()

recurrence_intervals() calculates the recurrence intervals based on how many recurrence interval orders is specified (see image below). Specifically, they are calculated as the timing difference between a discharge event in one (reference) motor unit and the nearest forward and nearest backward discharge events in another (event) motor unit. The motor unit used as the reference unit is the unit with fewer discharges. Order refers to how many discharges before and after we are including in our calculations. Default settings are for first order recurrence intervals as previous research has shown that false peaks are likely to appear with higher orders.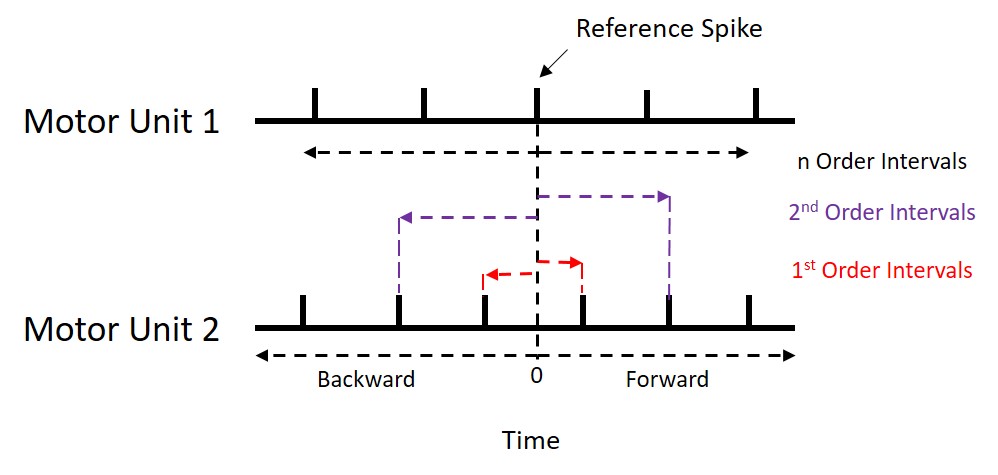

The function takes the vector arguments motor_unit_1 and motor_unit_2 containing activation times, along with an integer indicating the order. The code below calculates the time differences between the reference activation and the first and second forward and backward discharges from the event motor unit.

recur <- recurrence_intervals(motor_unit_1, motor_unit_2, order = 2)
names(recur)
#>  [1] "Reference_Unit"                 "Number_of_Reference_Discharges"
#>  [3] "Reference_ISI"                  "Mean_Reference_ISI"            
#>  [5] "Event_Unit"                     "Number_of_Event_Discharges"    
#>  [7] "Event_ISI"                      "Mean_Event_ISI"                
#>  [9] "Duration"                       "1"                             
#> [11] "2"

As you can see, various descriptors of the motor units are returned as a list. For example, the mean inter-spike interval (ISI) for the reference motor unit and the number of times the event motor unit discharged are returned. At the end are vectors containing all the recurrence intervals. In our example, with a recurrence interval order of 2, the vectors produced are denoted “1” and “2”. The first pair of numbers in vector [1] describes the recurrence interval time between the first reference activation and the first order activation of the event motor unit. The second pair of numbers indicates the recurrence interval between the second reference activation and the corresponding first order discharges from the event motor unit, and so on. For vector [2], pairs of numbers describes the recurrence interval between the reference discharge and the second order discharges from the event motor unit.

recur$'Reference_Unit'
#> [1] "motor_unit_2"
recur$Mean_Reference_ISI
#> [1] 0.098
recur$Number_of_Event_Discharges
#> [1] 443
head(recur$'1')
#> [1] -0.065  0.015 -0.022  0.045 -0.048  0.008

For demonstration purposes, we will only be using the first order intervals.

Discretize recurrence intervals with bin()

Only 2 arguments are needed for bin(); a vector containing the recurrence intervals we just calculated and a numeric indicating the bin size or width. Using unlist() will take our intervals from our list format and convert them into a vector format.

recur <- unlist(recur$`1`)
binned_data <- bin(recur, binwidth = 0.001)

A simple data frame is returned. Bin tells us how far before or after the discharge of our reference motor unit that the other motor unit discharged. Bin “0.000” represents the two motor units firing at the exact same time. Freq is the frequency of that interval occurring in the trial. Below we parse out from the data frame only the bins representing +/- 0.015 s around the reference motor unit discharge.

subset(binned_data, Bin >= -0.015 & Bin <= 0.015)
#>        Bin Freq
#> 87  -0.015    4
#> 88  -0.014    7
#> 89  -0.013   12
#> 90  -0.012    5
#> 91  -0.011    3
#> 92  -0.010    4
#> 93  -0.009    5
#> 94  -0.008   12
#> 95  -0.007   14
#> 96  -0.006    5
#> 97  -0.005   10
#> 98  -0.004   10
#> 99  -0.003    2
#> 100 -0.002   13
#> 101 -0.001    3
#> 102  0.000   21
#> 103  0.001   13
#> 104  0.002    1
#> 105  0.003    5
#> 106  0.004    4
#> 107  0.005    6
#> 108  0.006    4
#> 109  0.007    5
#> 110  0.008    7
#> 111  0.009    4
#> 112  0.010    4
#> 113  0.011    0
#> 114  0.012    9
#> 115  0.013    2
#> 116  0.014    4
#> 117  0.015    4

Visualization of histogram with plot_bins()

plot_bins() leverages ggplot2 to graph the binned recurrence intervals as a histogram. Mean bin size or average frequency of the bins is indicated as a red line on the graph.

plot_bins(binned_data)

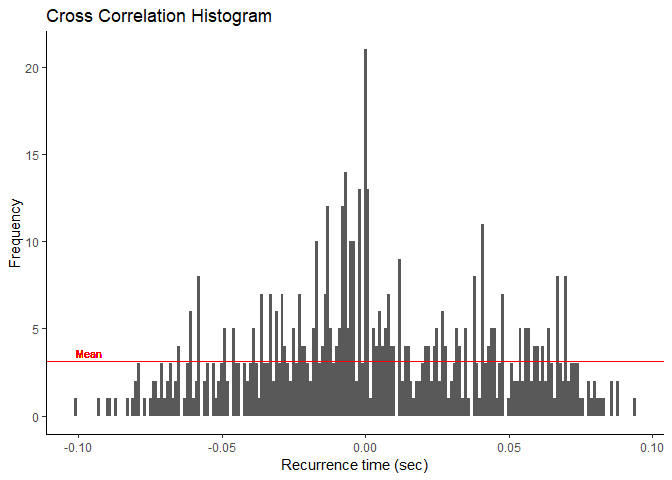From the graph, we can see that there are higher frequencies the nearer to “0.000” we get. This may indicate that there is a more than likely chance that these two motor units are functionally connected somehow. If there is a peak in this histogram, then our synchronization functions will determine where it is and calculate the various indices from it.

Synchronization functions

mu_synch() is the all-in-one function that calls both recurrence_intervals() and bin() to perform the initial analysis. It then uses the user-chosen methods for determining if and where there is a peak. More specifically, it uses these methods to find the upper and lower boundaries of a peak if there is one. “Visual”, “Cumsum”, and “Zscore” methods are described below and are available for peak determination. Alternatively, each method can be called individually using their own functions.

synch_data <- mu_synch(motor_unit_1, motor_unit_2, method = c("Visual", "Cumsum", "Zscore"), order = 1, binwidth = 0.001, plot = F)

A list is returned including the motor unit characteristic data and the 6 synchronization indices (described below) for each of the methods chosen.

names(synch_data)
## [1] "Data" "Visual Indices" "Zscore Indices" "Cumsum Indices"
synch_data$`Visual Indices`
## $`CIS`
## [1] 2.163168
## 
## $kprime
## [1] 3.79096
## 
## $kminus1
## [1] 2.79096
## 
## $E
## [1] 0.2110322
## 
## $S
## [1] 0.08638251
## 
## $SI
## [1] 0.2117218
## 
## $Peak.duration
## [1] 0.01
## 
## $Peak.center
## [1] 0
synch_data$`Zscore Indices`
#> $CIS
#> [1] 1.714933
#> 
#> $kprime
#> [1] 4.284502
#> 
#> $kminus1
#> [1] 3.284502
#> 
#> $E
#> [1] 0.1673037
#> 
#> $S
#> [1] 0.06848299
#> 
#> $SI
#> [1] 0.1678505
#> 
#> $Peak.duration
#> [1] NA
#> 
#> $Peak.center
#> [1] NA
synch_data$`Cumsum Indices`
#> $CIS
#> [1] 2.163168
#> 
#> $kprime
#> [1] 3.79096
#> 
#> $kminus1
#> [1] 2.79096
#> 
#> $E
#> [1] 0.2110322
#> 
#> $S
#> [1] 0.08638251
#> 
#> $SI
#> [1] 0.2117218
#> 
#> $Peak.duration
#> [1] 0.01
#> 
#> $Peak.center
#> [1] 0

Synchronization Index Formulas

  1. Common Input Strength (CIS) = extra counts in peak / duration of time both motor units are active (s)
  2. k’ = total counts in peak / expected counts in peak
  3. k’-1 = extra counts in peak / expected counts in peak
  4. E = extra counts in peak / number of reference discharges
  5. S = extra counts in peak / (number of reference discharges + number of event discharges))
  6. Synch Index (SI) = (extra counts in peak / (total counts in peak / 2))

Expected counts are the number of counts within the peak boundaries that we would expect to have if the two motor units were independent. This is usually calculated as the mean bin count of the baseline portion of the histogram (<= -0.06 s and >= 0.06 s). This is explained more in depth in the determination methods sections.

Peak location is also returned with the Synchronization Indices:

Visual Determination

Visual determination of peaks in a cross correlation histogram takes a more subjective approach than other automated detection algorithms. Investigators are usually asked where they see peaks, but as bin count or bin frequency can vary greatly, discerning areas of greater frequncy can be difficult for the human eye. To make it easier, the mean baseline bin frequency (considered the mean frequncy of bins >= -0.06 s and <= 0.06 s) is subtracted from each bin. Then the cumulative sum is taken from these normlized bins. This method allows for normally difficult to see increases in frequency (or peaks) to show up as deflections in the graph. The boundaries of these deflections are the boundaries of the peak. When called, this function automatically configures the normalized cumulative sum then leverages the dygraphs package to interactively display it for the user to view and determine peak boundaries.

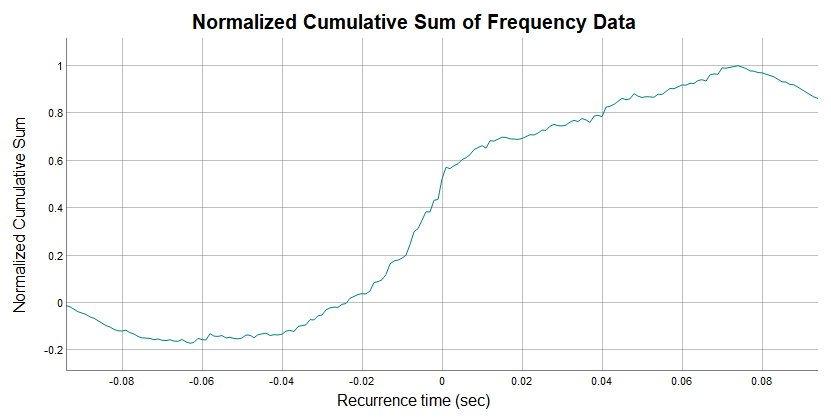
In the graph above you see the x-axis is just like the bins of the cross correlation histogram, representing the time difference between firings of the motor units. The y-axis notes the normalized cumulative sum values for each bin. The mouse can be used to drag a vertical cursor along the graph. This will display x and y values.

When the function is called, the user is prompted in the console to indicate whether they actually see a deflection in the graph near time “0.00” that may indicate a peak (y/n).

Is there a discernable change in slope or deflection near time 0 (y/n)? 
Enter the time (in sec) of the start of slope change (left or lower boundary of peak) of the graph:
Enter the time (in sec) of the end of slope change (right or upper boundary of peak) of the graph:

The synchronization function for visual determination is below. A list similar to mu_synch() is returned.

visual_mu_synch(motor_unit_1, motor_unit_2, order = 1, binwidth = 0.001, get_data = T, plot = F)

Cumsum Determination

The cumulative sum method is an automated method that does not require input by the user. Peak boundaries are determined as the bins associated with 10% and 90% of the range (maximum minus minimum) of the cumulative sum. The peak is considered significant if its mean bin count exceeds the sum of the mean and 1.96 * standard deviation of the baseline bins (<= -0.06 s and >= 0.06 s). If no significant peak is detected, a default +/- 0.005 s peak duration is used.

cumsum_mu_synch(motor_unit_1, motor_unit_2, order = 1, binwidth = 0.001, get_data = T, plot = F)

Z-score Determination

Another automated method for peak determination is the z-score method, which relies on the assumption that if two motor units are independent (i.e. no synchronization) then the cross correlation between them is random and the histogram would appear flat. So first, a random uniform distribution is used to produce a flat histogram and calculate a mean + 1.96 * standard deviation threshold for the experimental cross correlation histogram. Any bins in the experimental histogram within +/- 0.01 s of 0.000 that crosses the threshold are considered to be significantly greater than expected due to chance and subsequently used for analysis. If no peaks are detected, synchronization indices of 0 are returned. Because the z-score method tests each bin individually, peak bins are not necessarily adjacent. Therefore, peak duration and peak center are returned as NA.

zscore_mu_synch(motor_unit_1, motor_unit_2, order = 1, binwidth = 0.001, get_data = T, plot = F)

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.