The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.
lava

A general implementation of Structural Equation Models with latent variables (MLE, 2SLS, and composite likelihood estimators) with both continuous, censored, and ordinal outcomes (Holst and Budtz-Joergensen (2013) <10.1007/s00180-012-0344-y>). Mixture latent variable models and non-linear latent variable models (Holst and Budtz-Joergensen (2020) <10.1093/biostatistics/kxy082>). The package also provides methods for graph exploration (d-separation, back-door criterion), simulation of general non-linear latent variable models, and estimation of influence functions for a broad range of statistical models.
install.packages("lava", dependencies=TRUE)
library("lava")
demo("lava")For graphical capabilities the Rgraphviz package is
needed (first install the BiocManager package)
# install.packages("BiocManager")
BiocManager::install("Rgraphviz")or the igraph or visNetwork packages
install.packages("igraph")
install.packages("visNetwork")The development version of lava may also be installed
directly from github:
# install.packages("remotes")
remotes::install_github("kkholst/lava")To cite that lava package please use one of the
following references
Klaus K. Holst and Esben Budtz-Joergensen (2013). Linear Latent Variable Models: The lava-package. Computational Statistics 28 (4), pp 1385-1453. http://dx.doi.org/10.1007/s00180-012-0344-y
@article{lava,
title = {Linear Latent Variable Models: The lava-package},
author = {Klaus Kähler Holst and Esben Budtz-Jørgensen},
year = {2013},
volume = {28},
number = {4},
pages = {1385-1452},
journal = {Computational Statistics},
doi = {10.1007/s00180-012-0344-y}
}Klaus K. Holst and Esben Budtz-Jørgensen (2020). A two-stage estimation procedure for non-linear structural equation models. Biostatistics 21 (4), pp 676-691. http://dx.doi.org/10.1093/biostatistics/kxy082
@article{lava_nlin,
title = {A two-stage estimation procedure for non-linear structural equation models},
author = {Klaus Kähler Holst and Esben Budtz-Jørgensen},
journal = {Biostatistics},
year = {2020},
volume = {21},
number = {4},
pages = {676-691},
doi = {10.1093/biostatistics/kxy082},
}Specify structural equation models with two factors
m <- lvm()
regression(m) <- y1 + y2 + y3 ~ eta1
regression(m) <- z1 + z2 + z3 ~ eta2
latent(m) <- ~ eta1 + eta2
regression(m) <- eta2 ~ eta1 + x
regression(m) <- eta1 ~ x
labels(m) <- c(eta1=expression(eta[1]), eta2=expression(eta[2]))
plot(m)
Simulation
d <- sim(m, 100, seed=1)Estimation
e <- estimate(m, d)
e
#> Estimate Std. Error Z-value P-value
#> Measurements:
#> y2~eta1 0.95462 0.08083 11.80993 <1e-12
#> y3~eta1 0.98476 0.08922 11.03722 <1e-12
#> z2~eta2 0.97038 0.05368 18.07714 <1e-12
#> z3~eta2 0.95608 0.05643 16.94182 <1e-12
#> Regressions:
#> eta1~x 1.24587 0.11486 10.84694 <1e-12
#> eta2~eta1 0.95608 0.18008 5.30910 1.102e-07
#> eta2~x 1.11495 0.25228 4.41951 9.893e-06
#> Intercepts:
#> y2 -0.13896 0.12458 -1.11537 0.2647
#> y3 -0.07661 0.13869 -0.55241 0.5807
#> eta1 0.15801 0.12780 1.23644 0.2163
#> z2 -0.00441 0.14858 -0.02969 0.9763
#> z3 -0.15900 0.15731 -1.01076 0.3121
#> eta2 -0.14143 0.18380 -0.76949 0.4416
#> Residual Variances:
#> y1 0.69684 0.14858 4.69004
#> y2 0.89804 0.16630 5.40026
#> y3 1.22456 0.21182 5.78109
#> eta1 0.93620 0.19623 4.77084
#> z1 1.41422 0.26259 5.38570
#> z2 0.87569 0.19463 4.49934
#> z3 1.18155 0.22640 5.21883
#> eta2 1.24430 0.28992 4.29195Assessing goodness-of-fit, here the linearity between eta2 and eta1
(requires the gof package)
# install.packages("gof", repos="https://kkholst.github.io/r_repo/")
library("gof")
set.seed(1)
g <- cumres(e, eta2 ~ eta1)
plot(g)
Simulate non-linear model
m <- lvm(y1 + y2 + y3 ~ u, u ~ x)
transform(m,u2 ~ u) <- function(x) x^2
regression(m) <- z~u2+u
d <- sim(m,200,p=c("z"=-1, "z~u2"=-0.5), seed=1)Stage 1:
m1 <- lvm(c(y1[0:s], y2[0:s], y3[0:s]) ~ 1*u, u ~ x)
latent(m1) <- ~ u
(e1 <- estimate(m1, d))
#> Estimate Std. Error Z-value P-value
#> Regressions:
#> u~x 1.06998 0.08208 13.03542 <1e-12
#> Intercepts:
#> u -0.08871 0.08753 -1.01344 0.3108
#> Residual Variances:
#> y1 1.00054 0.07075 14.14214
#> u 1.19873 0.15503 7.73233Stage 2
pp <- function(mu,var,data,...) cbind(u=mu[,"u"], u2=mu[,"u"]^2+var["u","u"])
(e <- measurement.error(e1, z~1+x, data=d, predictfun=pp))
#> Estimate Std.Err 2.5% 97.5% P-value
#> (Intercept) -1.1181 0.13795 -1.3885 -0.8477 5.273e-16
#> x -0.0537 0.13213 -0.3127 0.2053 6.844e-01
#> u 1.0039 0.11504 0.7785 1.2294 2.609e-18
#> u2 -0.4718 0.05213 -0.5740 -0.3697 1.410e-19f <- function(p) p[1]+p["u"]*u+p["u2"]*u^2
u <- seq(-1, 1, length.out=100)
plot(e, f, data=data.frame(u))
Studying the small-sample properties of a mediation analysis
m <- lvm(y~x, c~1)
regression(m) <- y+x ~ z
eventTime(m) <- t~min(y=1, c=0)
transform(m,S~t+status) <- function(x) survival::Surv(x[,1],x[,2])plot(m)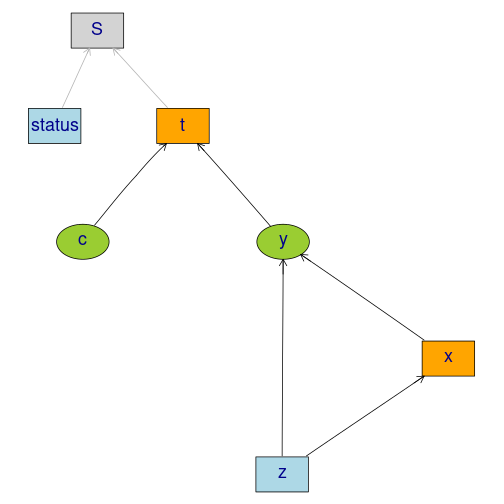
Simulate from model and estimate indirect effects
onerun <- function(...) {
d <- sim(m, 100)
m0 <- lvm(S~x+z, x~z)
e <- estimate(m0, d, estimator="glm")
vec(summary(effects(e, S~z))$coef[,1:2])
}
val <- sim(onerun, 100)
summary(val, estimate=1:4, se=5:8, short=TRUE)
#> 100 replications Time: 3.667s
#>
#> Total.Estimate Direct.Estimate Indirect.Estimate S~x~z.Estimate
#> Mean 1.97292 0.96537 1.00755 1.00755
#> SD 0.16900 0.18782 0.15924 0.15924
#> SE 0.18665 0.18090 0.16431 0.16431
#> SE/SD 1.10446 0.96315 1.03183 1.03183
#>
#> Min 1.47243 0.54497 0.54554 0.54554
#> 2.5% 1.63496 0.61228 0.64914 0.64914
#> 50% 1.95574 0.97154 0.99120 0.99120
#> 97.5% 2.27887 1.32443 1.27807 1.27807
#> Max 2.45746 1.49491 1.33446 1.33446
#>
#> Missing 0.00000 0.00000 0.00000 0.00000Add additional simulations and visualize results
val <- sim(val,500) ## Add 500 simulations
plot(val, estimate=c("Total.Estimate", "Indirect.Estimate"),
true=c(2, 1), se=c("Total.Std.Err", "Indirect.Std.Err"),
scatter.plot=TRUE)
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.