The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.
The itp package implements the Interpolate, Truncate, Project (ITP) root-finding algorithm of Oliveira and Takahashi (2021). Each iteration of the algorithm results in a bracketing interval for the root that is narrower than the previous interval. It’s performance compares favourably with existing methods on both well-behaved functions and ill-behaved functions while retaining the worst-case reliability of the bisection method. For details see the authors’ Kudos summary and the Wikipedia article ITP method.
We use three examples from Section 3 of Oliveira and Takahashi (2021)
to illustrate the use of the itp function. Each of these
functions has a root in the interval \((-1,
1)\). The function can be supplied either as an R function or as
an external pointer to a C++ function.
library(itp)The Lambert function \(l(x) = xe^x - 1\) is continuous.
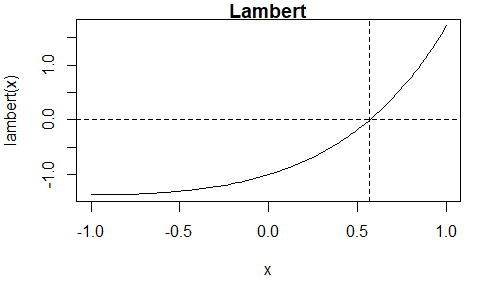
The itp function finds an estimate of the root, that is,
\(x^{\ast}\) for which \(f(x^{\ast})\) is (approximately) equal to
0. The algorithm continues until the length of the interval that
brackets the root is smaller than \(2
\epsilon\), where \(\epsilon\)
is a user-supplied tolerance. The default is \(\epsilon = 10^{-10}\).
First, we supply an R function that evaluates the Lambert function.
# Lambert, using an R function
lambert <- function(x) x * exp(x) - 1
itp(lambert, c(-1, 1))
#> function: lambert
#> root f(root) iterations
#> 0.5671 2.048e-12 8Now, we create an external pointer to a C++ function that has been
provided in the itp package and pass this pointer to the
function itp(). For more information see the Overview
of the itp package vignette.
# Lambert, using an external pointer to a C++ function
lambert_ptr <- xptr_create("lambert")
itp(lambert_ptr, c(-1, 1))
#> function: lambert_ptr
#> root f(root) iterations
#> 0.5671 2.048e-12 8itp_cAlso provided is the function itp_c, which is equivalent
to itp, but the calculations are performed entirely using
C++, and the arguments differ slightly: itp_c has a named
required argument pars rather than ... and it
does not have the arguments interval, f.a or
f.b.
# Calling itp_c()
res <- itp_c(lambert_ptr, pars = list(), a = -1, b = 1)
res
#> function:
#> root f(root) iterations
#> 0.5671 2.048e-12 8The staircase function \(s(x) = \lceil 10 x - 1 \rceil + 1/2\) is discontinuous.
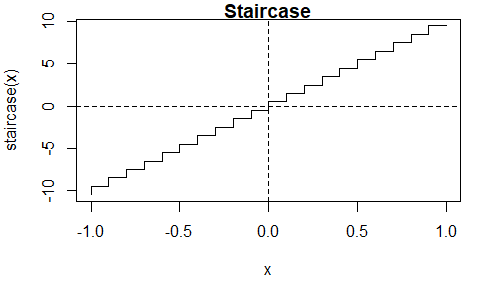
The itp function finds the discontinuity at \(x = 0\) at which the sign of the function
changes. The value of 0.5 returned for the root res$root is
the midpoint of the bracketing interval [res$a, res$b] at
convergence.
# Staircase
staircase <- function(x) ceiling(10 * x - 1) + 1 / 2
res <- itp(staircase, c(-1, 1))
print(res, all = TRUE)
#> function: staircase
#> root f(root) iterations a b f.a
#> 7.404e-11 0.5 31 0 1.481e-10 -0.5
#> f.b precision
#> 0.5 7.404e-11The Warsaw function \(w(x) = I(x > -1)\left(1 + \sin\left(\frac{1}{1+x}\right)\right)-1\) has multiple roots.
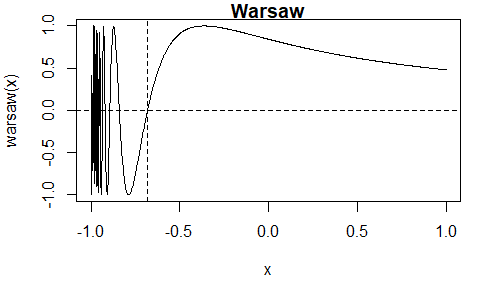
When the initial interval is \([-1,
1]\) the itp function finds the root \(x \approx -0.6817\). There are other roots
that could be found from a different initial interval.
# Warsaw
warsaw <- function(x) ifelse(x > -1, sin(1 / (x + 1)), -1)
itp(warsaw, c(-1, 1))
#> function: warsaw
#> root f(root) iterations
#> -0.6817 -5.472e-11 11To get the current released version from CRAN:
install.packages("itp")See the Overview
of the itp package vignette, which can also be accessed using
vignette("itp-vignette", package = "itp").
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.