The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.
flamingos is an open-source toolbox (available in R and in Matlab) for the simultaneous clustering and segmentation of heterogeneous functional data (i.e time-series ore more generally longitudinal data), with original and flexible functional latent variable models, fitted by unsupervised algorithms, including EM algorithms.
Our nice FLaMingos are mainly:
The models and algorithms are developped and written in Matlab by Faicel Chamroukhi, and translated and designed into R packages by Florian Lecocq, Marius Bartcus and Faicel Chamroukhi.
You can install the flamingos package from GitHub with:
# install.packages("devtools")
devtools::install_github("fchamroukhi/FLaMingos")To build vignettes for examples of usage, type the command below instead:
# install.packages("devtools")
devtools::install_github("fchamroukhi/FLaMingos",
build_opts = c("--no-resave-data", "--no-manual"),
build_vignettes = TRUE)Use the following command to display vignettes:
browseVignettes("flamingos")library(flamingos)data("toydataset")
x <- toydataset$x
Y <- t(toydataset[,2:ncol(toydataset)])
K <- 3 # Number of clusters
R <- 3 # Number of regimes (polynomial regression components)
p <- 1 # Degree of the polynomials
q <- 1 # Order of the logistic regression (by default 1 for contiguous segmentation)
variance_type <- "heteroskedastic" # "heteroskedastic" or "homoskedastic" model
n_tries <- 1
max_iter <- 1000
threshold <- 1e-5
verbose <- TRUE
verbose_IRLS <- FALSE
init_kmeans <- TRUE
mixrhlp <- emMixRHLP(X = x, Y = Y, K, R, p, q, variance_type, init_kmeans,
n_tries, max_iter, threshold, verbose, verbose_IRLS)
#> EM - mixRHLP: Iteration: 1 | log-likelihood: -18129.8169520025
#> EM - mixRHLP: Iteration: 2 | log-likelihood: -16642.732267463
#> EM - mixRHLP: Iteration: 3 | log-likelihood: -16496.947898833
#> EM - mixRHLP: Iteration: 4 | log-likelihood: -16391.6755568235
#> EM - mixRHLP: Iteration: 5 | log-likelihood: -16308.151649539
#> EM - mixRHLP: Iteration: 6 | log-likelihood: -16242.6749975019
#> EM - mixRHLP: Iteration: 7 | log-likelihood: -16187.9951484578
#> EM - mixRHLP: Iteration: 8 | log-likelihood: -16138.360050325
#> EM - mixRHLP: Iteration: 9 | log-likelihood: -16092.9430959116
#> EM - mixRHLP: Iteration: 10 | log-likelihood: -16053.588838999
#> EM - mixRHLP: Iteration: 11 | log-likelihood: -16020.7365667916
#> EM - mixRHLP: Iteration: 12 | log-likelihood: -15993.7513179937
#> EM - mixRHLP: Iteration: 13 | log-likelihood: -15972.7088032469
#> EM - mixRHLP: Iteration: 14 | log-likelihood: -15957.3889127412
#> EM - mixRHLP: Iteration: 15 | log-likelihood: -15946.5663566082
#> EM - mixRHLP: Iteration: 16 | log-likelihood: -15938.693534838
#> EM - mixRHLP: Iteration: 17 | log-likelihood: -15932.584112949
#> EM - mixRHLP: Iteration: 18 | log-likelihood: -15927.5299507605
#> EM - mixRHLP: Iteration: 19 | log-likelihood: -15923.1499635319
#> EM - mixRHLP: Iteration: 20 | log-likelihood: -15919.2392546398
#> EM - mixRHLP: Iteration: 21 | log-likelihood: -15915.6795793534
#> EM - mixRHLP: Iteration: 22 | log-likelihood: -15912.3944381959
#> EM - mixRHLP: Iteration: 23 | log-likelihood: -15909.327585346
#> EM - mixRHLP: Iteration: 24 | log-likelihood: -15906.4326405988
#> EM - mixRHLP: Iteration: 25 | log-likelihood: -15903.6678636145
#> EM - mixRHLP: Iteration: 26 | log-likelihood: -15900.9933370165
#> EM - mixRHLP: Iteration: 27 | log-likelihood: -15898.3692402859
#> EM - mixRHLP: Iteration: 28 | log-likelihood: -15895.7545341827
#> EM - mixRHLP: Iteration: 29 | log-likelihood: -15893.1056775993
#> EM - mixRHLP: Iteration: 30 | log-likelihood: -15890.3751610539
#> EM - mixRHLP: Iteration: 31 | log-likelihood: -15887.5097378815
#> EM - mixRHLP: Iteration: 32 | log-likelihood: -15884.4482946475
#> EM - mixRHLP: Iteration: 33 | log-likelihood: -15881.1193453446
#> EM - mixRHLP: Iteration: 34 | log-likelihood: -15877.4381561224
#> EM - mixRHLP: Iteration: 35 | log-likelihood: -15873.3037170772
#> EM - mixRHLP: Iteration: 36 | log-likelihood: -15868.595660791
#> EM - mixRHLP: Iteration: 37 | log-likelihood: -15863.171868441
#> EM - mixRHLP: Iteration: 38 | log-likelihood: -15856.8678694783
#> EM - mixRHLP: Iteration: 39 | log-likelihood: -15849.5002500459
#> EM - mixRHLP: Iteration: 40 | log-likelihood: -15840.8778843568
#> EM - mixRHLP: Iteration: 41 | log-likelihood: -15830.8267303162
#> EM - mixRHLP: Iteration: 42 | log-likelihood: -15819.2343887404
#> EM - mixRHLP: Iteration: 43 | log-likelihood: -15806.11425583
#> EM - mixRHLP: Iteration: 44 | log-likelihood: -15791.6651550126
#> EM - mixRHLP: Iteration: 45 | log-likelihood: -15776.2575311116
#> EM - mixRHLP: Iteration: 46 | log-likelihood: -15760.2525673176
#> EM - mixRHLP: Iteration: 47 | log-likelihood: -15743.6600428386
#> EM - mixRHLP: Iteration: 48 | log-likelihood: -15725.8494727209
#> EM - mixRHLP: Iteration: 49 | log-likelihood: -15705.5392028324
#> EM - mixRHLP: Iteration: 50 | log-likelihood: -15681.0330055801
#> EM - mixRHLP: Iteration: 51 | log-likelihood: -15650.7058006772
#> EM - mixRHLP: Iteration: 52 | log-likelihood: -15614.1891628978
#> EM - mixRHLP: Iteration: 53 | log-likelihood: -15574.3209962234
#> EM - mixRHLP: Iteration: 54 | log-likelihood: -15536.9561042095
#> EM - mixRHLP: Iteration: 55 | log-likelihood: -15505.9888676546
#> EM - mixRHLP: Iteration: 56 | log-likelihood: -15480.3479747868
#> EM - mixRHLP: Iteration: 57 | log-likelihood: -15456.7432033066
#> EM - mixRHLP: Iteration: 58 | log-likelihood: -15432.855894347
#> EM - mixRHLP: Iteration: 59 | log-likelihood: -15408.4123139152
#> EM - mixRHLP: Iteration: 60 | log-likelihood: -15384.7708355233
#> EM - mixRHLP: Iteration: 61 | log-likelihood: -15363.3704926307
#> EM - mixRHLP: Iteration: 62 | log-likelihood: -15344.3247788467
#> EM - mixRHLP: Iteration: 63 | log-likelihood: -15326.444200793
#> EM - mixRHLP: Iteration: 64 | log-likelihood: -15308.1502066517
#> EM - mixRHLP: Iteration: 65 | log-likelihood: -15288.3650661699
#> EM - mixRHLP: Iteration: 66 | log-likelihood: -15267.1380314858
#> EM - mixRHLP: Iteration: 67 | log-likelihood: -15245.8151021308
#> EM - mixRHLP: Iteration: 68 | log-likelihood: -15226.3007649639
#> EM - mixRHLP: Iteration: 69 | log-likelihood: -15209.9671868432
#> EM - mixRHLP: Iteration: 70 | log-likelihood: -15197.3697193674
#> EM - mixRHLP: Iteration: 71 | log-likelihood: -15187.8845852548
#> EM - mixRHLP: Iteration: 72 | log-likelihood: -15180.4065779427
#> EM - mixRHLP: Iteration: 73 | log-likelihood: -15174.1897193241
#> EM - mixRHLP: Iteration: 74 | log-likelihood: -15168.8680084075
#> EM - mixRHLP: Iteration: 75 | log-likelihood: -15164.1615627415
#> EM - mixRHLP: Iteration: 76 | log-likelihood: -15159.6679572457
#> EM - mixRHLP: Iteration: 77 | log-likelihood: -15155.1488045656
#> EM - mixRHLP: Iteration: 78 | log-likelihood: -15150.9231858137
#> EM - mixRHLP: Iteration: 79 | log-likelihood: -15147.2212168192
#> EM - mixRHLP: Iteration: 80 | log-likelihood: -15144.078942659
#> EM - mixRHLP: Iteration: 81 | log-likelihood: -15141.3516305636
#> EM - mixRHLP: Iteration: 82 | log-likelihood: -15138.8602529876
#> EM - mixRHLP: Iteration: 83 | log-likelihood: -15136.5059345662
#> EM - mixRHLP: Iteration: 84 | log-likelihood: -15134.2384537766
#> EM - mixRHLP: Iteration: 85 | log-likelihood: -15132.0298589309
#> EM - mixRHLP: Iteration: 86 | log-likelihood: -15129.8608706576
#> EM - mixRHLP: Iteration: 87 | log-likelihood: -15127.7157936565
#> EM - mixRHLP: Iteration: 88 | log-likelihood: -15125.5797196054
#> EM - mixRHLP: Iteration: 89 | log-likelihood: -15123.4372146492
#> EM - mixRHLP: Iteration: 90 | log-likelihood: -15121.2712280838
#> EM - mixRHLP: Iteration: 91 | log-likelihood: -15119.0622569401
#> EM - mixRHLP: Iteration: 92 | log-likelihood: -15116.7874031382
#> EM - mixRHLP: Iteration: 93 | log-likelihood: -15114.4192658119
#> EM - mixRHLP: Iteration: 94 | log-likelihood: -15111.9245293407
#> EM - mixRHLP: Iteration: 95 | log-likelihood: -15109.262047444
#> EM - mixRHLP: Iteration: 96 | log-likelihood: -15106.3802520661
#> EM - mixRHLP: Iteration: 97 | log-likelihood: -15103.2137059945
#> EM - mixRHLP: Iteration: 98 | log-likelihood: -15099.6787565231
#> EM - mixRHLP: Iteration: 99 | log-likelihood: -15095.6664401258
#> EM - mixRHLP: Iteration: 100 | log-likelihood: -15091.0341403017
#> EM - mixRHLP: Iteration: 101 | log-likelihood: -15085.5952981967
#> EM - mixRHLP: Iteration: 102 | log-likelihood: -15079.1100803411
#> EM - mixRHLP: Iteration: 103 | log-likelihood: -15071.2863215881
#> EM - mixRHLP: Iteration: 104 | log-likelihood: -15061.8155026615
#> EM - mixRHLP: Iteration: 105 | log-likelihood: -15050.4931948422
#> EM - mixRHLP: Iteration: 106 | log-likelihood: -15037.4728804542
#> EM - mixRHLP: Iteration: 107 | log-likelihood: -15023.5663638262
#> EM - mixRHLP: Iteration: 108 | log-likelihood: -15010.227713049
#> EM - mixRHLP: Iteration: 109 | log-likelihood: -14998.9216243488
#> EM - mixRHLP: Iteration: 110 | log-likelihood: -14990.3428946115
#> EM - mixRHLP: Iteration: 111 | log-likelihood: -14984.2931646741
#> EM - mixRHLP: Iteration: 112 | log-likelihood: -14980.0317050997
#> EM - mixRHLP: Iteration: 113 | log-likelihood: -14976.7574542595
#> EM - mixRHLP: Iteration: 114 | log-likelihood: -14973.9768267566
#> EM - mixRHLP: Iteration: 115 | log-likelihood: -14971.5304235767
#> EM - mixRHLP: Iteration: 116 | log-likelihood: -14969.3710026547
#> EM - mixRHLP: Iteration: 117 | log-likelihood: -14967.3301314624
#> EM - mixRHLP: Iteration: 118 | log-likelihood: -14965.1319732928
#> EM - mixRHLP: Iteration: 119 | log-likelihood: -14962.818626259
#> EM - mixRHLP: Iteration: 120 | log-likelihood: -14961.1657986148
#> EM - mixRHLP: Iteration: 121 | log-likelihood: -14960.1001793804
#> EM - mixRHLP: Iteration: 122 | log-likelihood: -14959.2029493404
#> EM - mixRHLP: Iteration: 123 | log-likelihood: -14958.3643653619
#> EM - mixRHLP: Iteration: 124 | log-likelihood: -14957.5579272948
#> EM - mixRHLP: Iteration: 125 | log-likelihood: -14956.7769206505
#> EM - mixRHLP: Iteration: 126 | log-likelihood: -14956.0220832192
#> EM - mixRHLP: Iteration: 127 | log-likelihood: -14955.2990068376
#> EM - mixRHLP: Iteration: 128 | log-likelihood: -14954.6080936987
#> EM - mixRHLP: Iteration: 129 | log-likelihood: -14953.9546052572
#> EM - mixRHLP: Iteration: 130 | log-likelihood: -14953.3424683065
#> EM - mixRHLP: Iteration: 131 | log-likelihood: -14952.7742704947
#> EM - mixRHLP: Iteration: 132 | log-likelihood: -14952.2512735504
#> EM - mixRHLP: Iteration: 133 | log-likelihood: -14951.7732467988
#> EM - mixRHLP: Iteration: 134 | log-likelihood: -14951.3384384815
#> EM - mixRHLP: Iteration: 135 | log-likelihood: -14950.9439547413
#> EM - mixRHLP: Iteration: 136 | log-likelihood: -14950.5860673359
#> EM - mixRHLP: Iteration: 137 | log-likelihood: -14950.2605961901
#> EM - mixRHLP: Iteration: 138 | log-likelihood: -14949.9632302133
#> EM - mixRHLP: Iteration: 139 | log-likelihood: -14949.6897803656
#> EM - mixRHLP: Iteration: 140 | log-likelihood: -14949.4363440458
#> EM - mixRHLP: Iteration: 141 | log-likelihood: -14949.1993934329
#> EM - mixRHLP: Iteration: 142 | log-likelihood: -14948.9758045711
#> EM - mixRHLP: Iteration: 143 | log-likelihood: -14948.7628462595
#> EM - mixRHLP: Iteration: 144 | log-likelihood: -14948.5581447387
#> EM - mixRHLP: Iteration: 145 | log-likelihood: -14948.3596363733
#> EM - mixRHLP: Iteration: 146 | log-likelihood: -14948.1655161518
#> EM - mixRHLP: Iteration: 147 | log-likelihood: -14947.9741866833
#> EM - mixRHLP: Iteration: 148 | log-likelihood: -14947.7842100466
#> EM - mixRHLP: Iteration: 149 | log-likelihood: -14947.5942633197
#> EM - mixRHLP: Iteration: 150 | log-likelihood: -14947.4030977377
#> EM - mixRHLP: Iteration: 151 | log-likelihood: -14947.2095010109
#> EM - mixRHLP: Iteration: 152 | log-likelihood: -14947.0122620331
#> EM - mixRHLP: Iteration: 153 | log-likelihood: -14946.8101371804
#> EM - mixRHLP: Iteration: 154 | log-likelihood: -14946.6018173877
#> EM - mixRHLP: Iteration: 155 | log-likelihood: -14946.3858952193
#> EM - mixRHLP: Iteration: 156 | log-likelihood: -14946.1608312027
#> EM - mixRHLP: Iteration: 157 | log-likelihood: -14945.9249187549
#> EM - mixRHLP: Iteration: 158 | log-likelihood: -14945.676247118
#> EM - mixRHLP: Iteration: 159 | log-likelihood: -14945.4126618353
#> EM - mixRHLP: Iteration: 160 | log-likelihood: -14945.1317224602
#> EM - mixRHLP: Iteration: 161 | log-likelihood: -14944.8306573941
#> EM - mixRHLP: Iteration: 162 | log-likelihood: -14944.5063160023
#> EM - mixRHLP: Iteration: 163 | log-likelihood: -14944.1551184229
#> EM - mixRHLP: Iteration: 164 | log-likelihood: -14943.7730037188
#> EM - mixRHLP: Iteration: 165 | log-likelihood: -14943.355377134
#> EM - mixRHLP: Iteration: 166 | log-likelihood: -14942.8970570836
#> EM - mixRHLP: Iteration: 167 | log-likelihood: -14942.3922219831
#> EM - mixRHLP: Iteration: 168 | log-likelihood: -14941.8343559995
#> EM - mixRHLP: Iteration: 169 | log-likelihood: -14941.2161912546
#> EM - mixRHLP: Iteration: 170 | log-likelihood: -14940.5296397031
#> EM - mixRHLP: Iteration: 171 | log-likelihood: -14939.7657190993
#> EM - mixRHLP: Iteration: 172 | log-likelihood: -14938.9144460343
#> EM - mixRHLP: Iteration: 173 | log-likelihood: -14937.9647057519
#> EM - mixRHLP: Iteration: 174 | log-likelihood: -14936.9040831122
#> EM - mixRHLP: Iteration: 175 | log-likelihood: -14935.7186499891
#> EM - mixRHLP: Iteration: 176 | log-likelihood: -14934.3927038884
#> EM - mixRHLP: Iteration: 177 | log-likelihood: -14932.9084527435
#> EM - mixRHLP: Iteration: 178 | log-likelihood: -14931.245639997
#> EM - mixRHLP: Iteration: 179 | log-likelihood: -14929.3811026273
#> EM - mixRHLP: Iteration: 180 | log-likelihood: -14927.2882537299
#> EM - mixRHLP: Iteration: 181 | log-likelihood: -14924.9364821865
#> EM - mixRHLP: Iteration: 182 | log-likelihood: -14922.2904675358
#> EM - mixRHLP: Iteration: 183 | log-likelihood: -14919.3094231961
#> EM - mixRHLP: Iteration: 184 | log-likelihood: -14915.9463144684
#> EM - mixRHLP: Iteration: 185 | log-likelihood: -14912.1471647651
#> EM - mixRHLP: Iteration: 186 | log-likelihood: -14907.8506901999
#> EM - mixRHLP: Iteration: 187 | log-likelihood: -14902.9887290339
#> EM - mixRHLP: Iteration: 188 | log-likelihood: -14897.4883102736
#> EM - mixRHLP: Iteration: 189 | log-likelihood: -14891.27676833
#> EM - mixRHLP: Iteration: 190 | log-likelihood: -14884.2919447409
#> EM - mixRHLP: Iteration: 191 | log-likelihood: -14876.4995909623
#> EM - mixRHLP: Iteration: 192 | log-likelihood: -14867.9179321727
#> EM - mixRHLP: Iteration: 193 | log-likelihood: -14858.6442978196
#> EM - mixRHLP: Iteration: 194 | log-likelihood: -14848.8804338117
#> EM - mixRHLP: Iteration: 195 | log-likelihood: -14838.9872847758
#> EM - mixRHLP: Iteration: 196 | log-likelihood: -14829.6292321768
#> EM - mixRHLP: Iteration: 197 | log-likelihood: -14821.8717823403
#> EM - mixRHLP: Iteration: 198 | log-likelihood: -14816.6461672058
#> EM - mixRHLP: Iteration: 199 | log-likelihood: -14813.7497363742
#> EM - mixRHLP: Iteration: 200 | log-likelihood: -14812.2267827519
#> EM - mixRHLP: Iteration: 201 | log-likelihood: -14811.4198287137
#> EM - mixRHLP: Iteration: 202 | log-likelihood: -14811.0049217051
#> EM - mixRHLP: Iteration: 203 | log-likelihood: -14810.7960368513
#> EM - mixRHLP: Iteration: 204 | log-likelihood: -14810.6883875777
mixrhlp$summary()
#> ------------------------
#> Fitted mixRHLP model
#> ------------------------
#>
#> MixRHLP model with K = 3 clusters and R = 3 regimes:
#>
#> log-likelihood nu AIC BIC ICL
#> -14810.69 41 -14851.69 -14880.41 -14880.41
#>
#> Clustering table (Number of curves in each clusters):
#>
#> 1 2 3
#> 10 10 10
#>
#> Mixing probabilities (cluster weights):
#> 1 2 3
#> 0.3333333 0.3333333 0.3333333
#>
#>
#> --------------------
#> Cluster 1 (k = 1):
#>
#> Regression coefficients for each regime/segment r (r=1...R):
#>
#> Beta(r = 1) Beta(r = 2) Beta(r = 3)
#> 1 4.96556671 6.7326717 4.8807183
#> X^1 0.08880479 0.4984443 0.1350271
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9559969 1.03849 0.9506928
#>
#> --------------------
#> Cluster 2 (k = 2):
#>
#> Regression coefficients for each regime/segment r (r=1...R):
#>
#> Beta(r = 1) Beta(r = 2) Beta(r = 3)
#> 1 6.8902863 5.1134337 3.90153421
#> X^1 0.9265632 -0.3959402 0.08748466
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.981915 0.9787717 0.9702211
#>
#> --------------------
#> Cluster 3 (k = 3):
#>
#> Regression coefficients for each regime/segment r (r=1...R):
#>
#> Beta(r = 1) Beta(r = 2) Beta(r = 3)
#> 1 6.3513369 4.214736 6.6536553
#> X^1 -0.2449377 0.839666 0.1024863
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9498285 0.9270384 1.001413
mixrhlp$plot()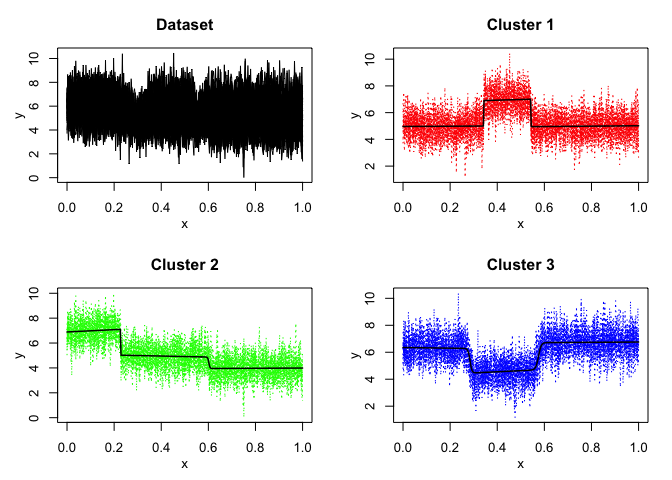
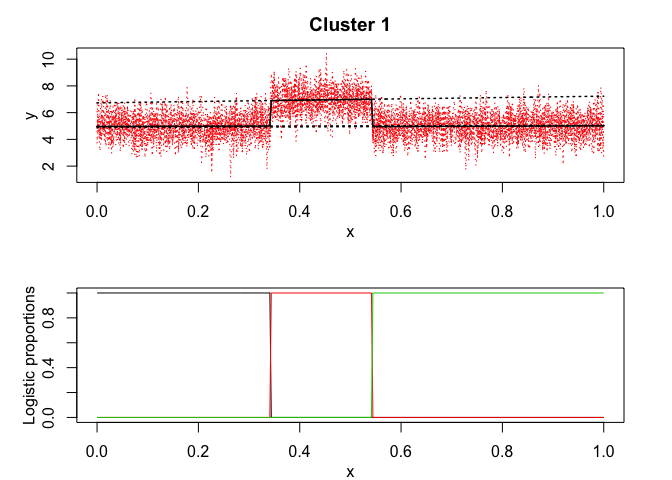
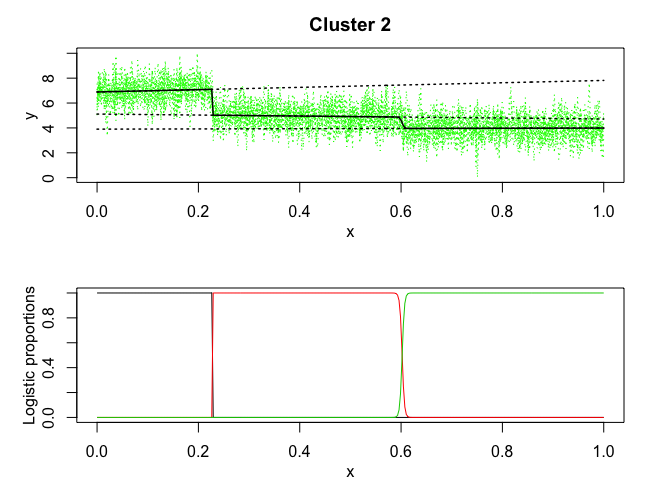
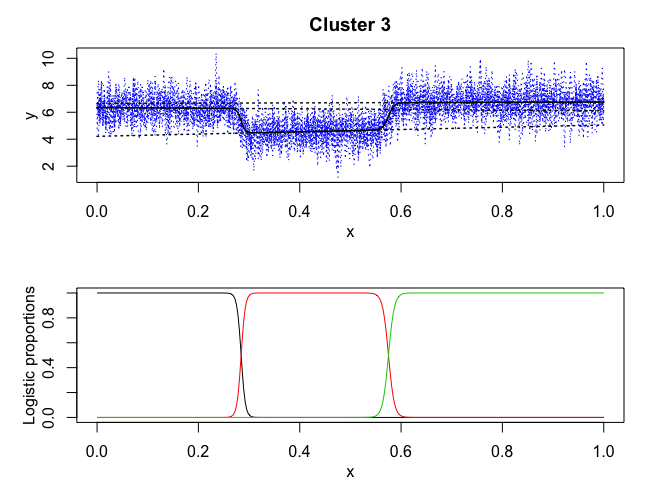
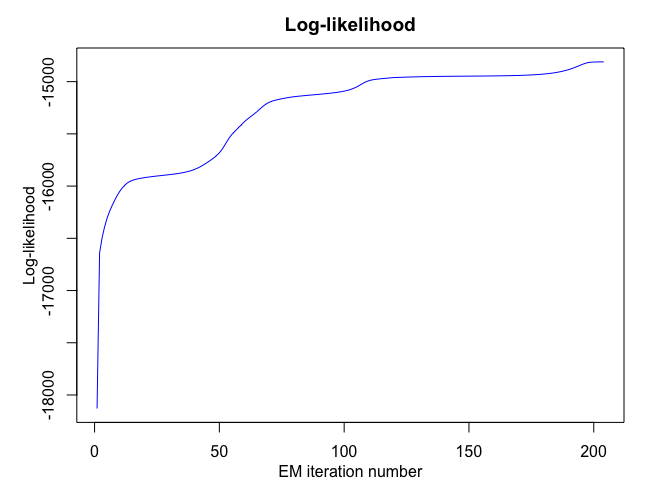
data("toydataset")
Y <- t(toydataset[,2:ncol(toydataset)])
K <- 3 # Number of clusters
R <- 3 # Number of regimes (HMM states)
variance_type <- "heteroskedastic" # "heteroskedastic" or "homoskedastic" model
ordered_states <- TRUE
n_tries <- 1
max_iter <- 1000
init_kmeans <- TRUE
threshold <- 1e-6
verbose <- TRUE
mixhmm <- emMixHMM(Y = Y, K, R, variance_type, ordered_states, init_kmeans,
n_tries, max_iter, threshold, verbose)
#> EM - mixHMMs: Iteration: 1 | log-likelihood: -19054.7157954833
#> EM - mixHMMs: Iteration: 2 | log-likelihood: -15386.7973253636
#> EM - mixHMMs: Iteration: 3 | log-likelihood: -15141.8435629464
#> EM - mixHMMs: Iteration: 4 | log-likelihood: -15058.7251666378
#> EM - mixHMMs: Iteration: 5 | log-likelihood: -15055.5058566489
#> EM - mixHMMs: Iteration: 6 | log-likelihood: -15055.4877310423
#> EM - mixHMMs: Iteration: 7 | log-likelihood: -15055.4876146553
mixhmm$summary()
#> -----------------------
#> Fitted mixHMM model
#> -----------------------
#>
#> MixHMM model with K = 3 clusters and R = 3 regimes:
#>
#> log-likelihood nu AIC BIC
#> -15055.49 41 -15096.49 -15125.21
#>
#> Clustering table (Number of curves in each clusters):
#>
#> 1 2 3
#> 10 10 10
#>
#> Mixing probabilities (cluster weights):
#> 1 2 3
#> 0.3333333 0.3333333 0.3333333
#>
#>
#> -------------------
#> Cluster 1 (k = 1):
#>
#> Means:
#>
#> r = 1 r = 2 r = 3
#> 7.00202 4.964273 3.979626
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9858726 0.9884542 0.9651437
#>
#> -------------------
#> Cluster 2 (k = 2):
#>
#> Means:
#>
#> r = 1 r = 2 r = 3
#> 4.987066 6.963998 4.987279
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9578459 1.045573 0.952294
#>
#> -------------------
#> Cluster 3 (k = 3):
#>
#> Means:
#>
#> r = 1 r = 2 r = 3
#> 6.319189 4.583954 6.722627
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9571803 0.9504731 1.01553
mixhmm$plot()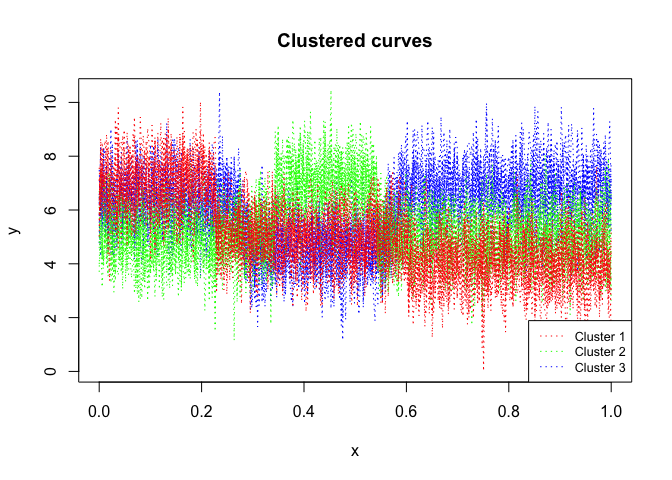
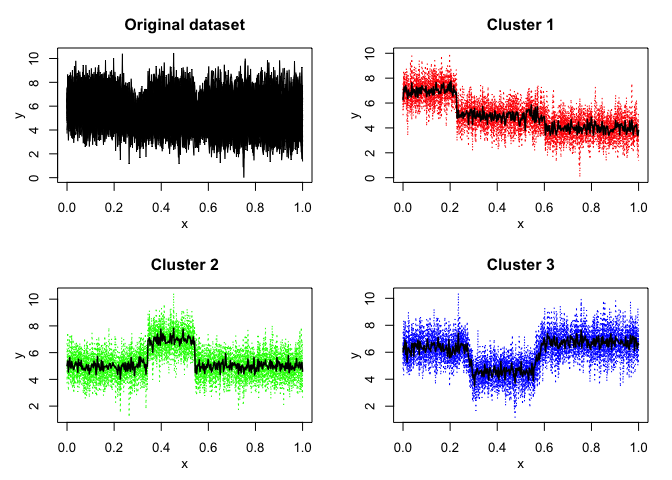
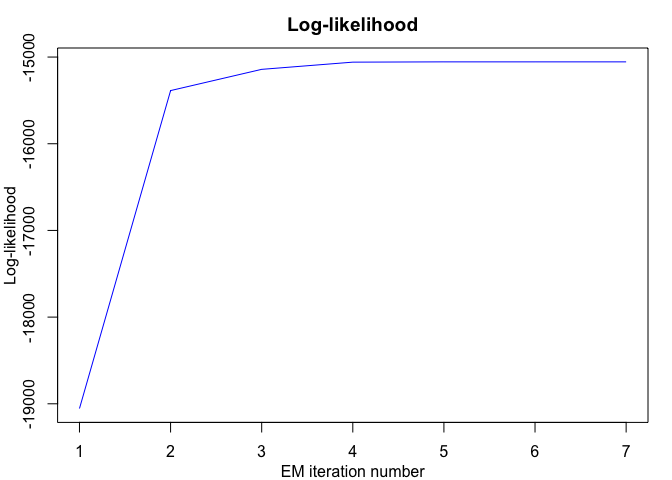
data("toydataset")
x <- toydataset$x
Y <- t(toydataset[,2:ncol(toydataset)])
K <- 3 # Number of clusters
R <- 3 # Number of regimes/states
p <- 1 # Degree of the polynomial regression
variance_type <- "heteroskedastic" # "heteroskedastic" or "homoskedastic" model
ordered_states <- TRUE
n_tries <- 1
max_iter <- 1000
init_kmeans <- TRUE
threshold <- 1e-6
verbose <- TRUE
mixhmmr <- emMixHMMR(X = x, Y = Y, K, R, p, variance_type, ordered_states,
init_kmeans, n_tries, max_iter, threshold, verbose)
#> EM - mixHMMR: Iteration: 1 || log-likelihood: -18975.6323298895
#> EM - mixHMMR: Iteration: 2 || log-likelihood: -15198.5811534058
#> EM - mixHMMR: Iteration: 3 || log-likelihood: -15118.0350455527
#> EM - mixHMMR: Iteration: 4 || log-likelihood: -15086.2933826057
#> EM - mixHMMR: Iteration: 5 || log-likelihood: -15084.2502053712
#> EM - mixHMMR: Iteration: 6 || log-likelihood: -15083.7770153797
#> EM - mixHMMR: Iteration: 7 || log-likelihood: -15083.3586992156
#> EM - mixHMMR: Iteration: 8 || log-likelihood: -15082.8291034608
#> EM - mixHMMR: Iteration: 9 || log-likelihood: -15082.2407744542
#> EM - mixHMMR: Iteration: 10 || log-likelihood: -15081.6808462523
#> EM - mixHMMR: Iteration: 11 || log-likelihood: -15081.175618676
#> EM - mixHMMR: Iteration: 12 || log-likelihood: -15080.5819574865
#> EM - mixHMMR: Iteration: 13 || log-likelihood: -15079.3118011276
#> EM - mixHMMR: Iteration: 14 || log-likelihood: -15076.8073408977
#> EM - mixHMMR: Iteration: 15 || log-likelihood: -15073.8399600893
#> EM - mixHMMR: Iteration: 16 || log-likelihood: -15067.6884092484
#> EM - mixHMMR: Iteration: 17 || log-likelihood: -15054.9127597414
#> EM - mixHMMR: Iteration: 18 || log-likelihood: -15049.4000307536
#> EM - mixHMMR: Iteration: 19 || log-likelihood: -15049.0221351022
#> EM - mixHMMR: Iteration: 20 || log-likelihood: -15048.997021329
#> EM - mixHMMR: Iteration: 21 || log-likelihood: -15048.9949507534
mixhmmr$summary()
#> ------------------------
#> Fitted mixHMMR model
#> ------------------------
#>
#> MixHMMR model with K = 3 clusters and R = 3 regimes:
#>
#> log-likelihood nu AIC BIC ICL
#> -15048.99 50 -15098.99 -15134.02 -15134.02
#>
#> Clustering table (Number of curves in each clusters):
#>
#> 1 2 3
#> 10 10 10
#>
#> Mixing probabilities (cluster weights):
#> 1 2 3
#> 0.3333333 0.3333333 0.3333333
#>
#>
#> --------------------
#> Cluster 1 (k = 1):
#>
#> Regression coefficients for each regime/segment r (r=1...R):
#>
#> Beta(r = 1) Beta(r = 2) Beta(r = 3)
#> 1 6.870328 5.1511267 3.9901300
#> X^1 1.204150 -0.4601777 -0.0155753
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9776399 0.9895623 0.96457
#>
#> --------------------
#> Cluster 2 (k = 2):
#>
#> Regression coefficients for each regime/segment r (r=1...R):
#>
#> Beta(r = 1) Beta(r = 2) Beta(r = 3)
#> 1 4.9512819 6.8393804 4.9076599
#> X^1 0.2099508 0.2822775 0.1031626
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9576192 1.045043 0.952047
#>
#> --------------------
#> Cluster 3 (k = 3):
#>
#> Regression coefficients for each regime/segment r (r=1...R):
#>
#> Beta(r = 1) Beta(r = 2) Beta(r = 3)
#> 1 6.3552432 4.2868818 6.5327846
#> X^1 -0.2865404 0.6907212 0.2429291
#>
#> Variances:
#>
#> Sigma2(r = 1) Sigma2(r = 2) Sigma2(r = 3)
#> 0.9587975 0.9481068 1.01388
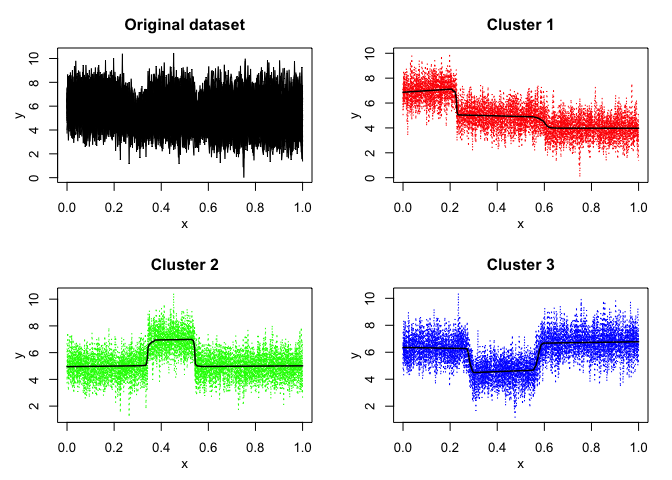
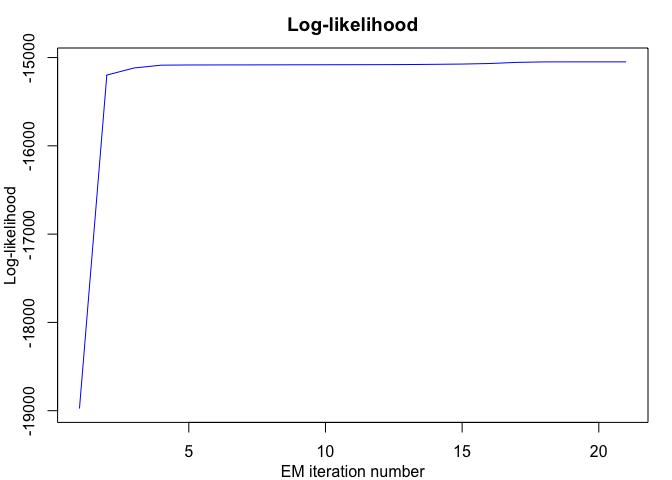
mixhmmr$plot()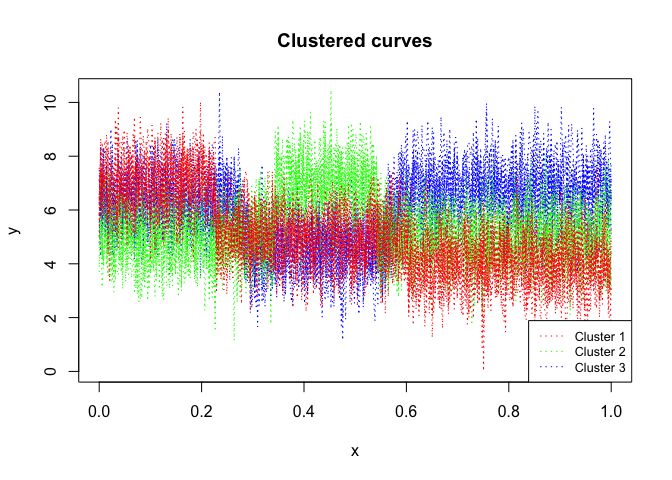
Chamroukhi, Faicel, and Hien D. Nguyen. 2019. “Model-Based Clustering and Classification of Functional Data.” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. https://chamroukhi.com/papers/MBCC-FDA.pdf.
Chamroukhi, F. 2016. “Unsupervised Learning of Regression Mixture Models with Unknown Number of Components.” Journal of Statistical Computation and Simulation 86 (November): 2308–34. https://chamroukhi.com/papers/Chamroukhi-JSCS-2015.pdf.
Chamroukhi, Faicel. 2016. “Piecewise Regression Mixture for Simultaneous Functional Data Clustering and Optimal Segmentation.” Journal of Classification 33 (3): 374–411. https://chamroukhi.com/papers/Chamroukhi-PWRM-JournalClassif-2016.pdf.
Chamroukhi, F. 2015. “Statistical Learning of Latent Data Models for Complex Data Analysis.” Habilitation Thesis (HDR), Université de Toulon. https://chamroukhi.com/Dossier/FChamroukhi-Habilitation.pdf.
Chamroukhi, F., H. Glotin, and A. Samé. 2013. “Model-Based Functional Mixture Discriminant Analysis with Hidden Process Regression for Curve Classification.” Neurocomputing 112: 153–63. https://chamroukhi.com/papers/chamroukhi_et_al_neucomp2013a.pdf.
Chamroukhi, F., and H. Glotin. 2012. “Mixture Model-Based Functional Discriminant Analysis for Curve Classification.” In Proceedings of the International Joint Conference on Neural Networks (IJCNN), IEEE, 1–8. Brisbane, Australia. https://chamroukhi.com/papers/Chamroukhi-ijcnn-2012.pdf.
Samé, A., F. Chamroukhi, Gérard Govaert, and P. Aknin. 2011. “Model-Based Clustering and Segmentation of Time Series with Changes in Regime.” Advances in Data Analysis and Classification 5 (4): 301–21. https://chamroukhi.com/papers/adac-2011.pdf.
Chamroukhi, F., A. Samé, P. Aknin, and G. Govaert. 2011. “Model-Based Clustering with Hidden Markov Model Regression for Time Series with Regime Changes.” In Proceedings of the International Joint Conference on Neural Networks (IJCNN), IEEE, 2814–21. https://chamroukhi.com/papers/Chamroukhi-ijcnn-2011.pdf.
Chamroukhi, F., A. Samé, G. Govaert, and P. Aknin. 2010. “A Hidden Process Regression Model for Functional Data Description. Application to Curve Discrimination.” Neurocomputing 73 (7-9): 1210–21. https://chamroukhi.com/papers/chamroukhi_neucomp_2010.pdf.
Chamroukhi, F. 2010. “Hidden Process Regression for Curve Modeling, Classification and Tracking.” Ph.D. Thesis, Université de Technologie de Compiègne. https://chamroukhi.com/papers/FChamroukhi-Thesis.pdf.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.