The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

bratteli

Bratteli graphs.

This package deals with Bratteli graphs. In every function of the package, the Bratteli graph is given by a function returning for a level n of the graph the incidence matrix of the graph between level n and level n+1: the (i,j)-entry of this matrix is the number of edges between the i-th vertex at level n and the j-th vertex at level n+1.

For example, the binary tree is defined by:

tree <- function(n) {
  M <- matrix(0, nrow = 2^n, ncol = 2^(n+1))
  for(i in 1:nrow(M)) {
    M[i, ][c( 2*(i-1)+1, 2*(i-1)+2 )] <- 1
  }
  M
}

The function bratteliGraph generates some LaTeX code which renders the graph up to a given level:

bratteliGraph("binaryTree.tex", tree, 3)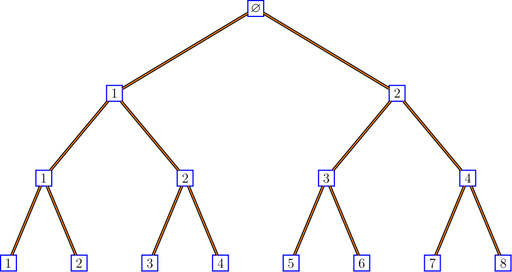

If you don’t like the style, you are free to modify the LaTeX code.

Here is a binary tree with double edges:

tree2 <- function(n) {
  M <- matrix(0, nrow = 2^n, ncol = 2^(n+1))
  for(i in 1:nrow(M)) {
    M[i, ][c( 2*(i-1)+1, 2*(i-1)+2 )] <- 2
  }
  M
}
bratteliGraph("binaryTree2.tex", tree2, 3)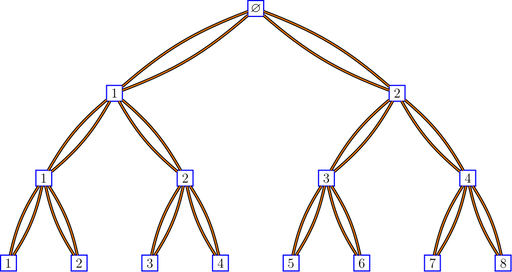

Here is the code for the Pascal graph:

Pascal <- function(n) {
  M <- matrix(0, nrow = n+1, ncol = n+2)
  for(i in 1:(n+1)) {
    M[i, ][c( i, i+1L )] <- 1
  }
  M
}

The dimension of a vertex of a Bratteli graph is the number of paths of the graph going from the root vertex to this vertex. The function bratteliDimensions of the package computes these numbers:

library(bratteli)
bratteliDimensions(Pascal, 3)

## [[1]]
## [1] "1" "1"
## 
## [[2]]
## [1] "1" "2" "1"
## 
## [[3]]
## [1] "1" "3" "3" "1"

Bratteli graphs are of interest to ergodicians, and particularly to Vershik, who introduced the intrinsic kernels of a Bratteli graph and the intrinsic distance between the vertices of a Bratteli graph. Here is a picture of the Pascal graph showing the intrinsic kernels:

bratteliGraph("Pascal.tex", Pascal, 3, edgelabels = "kernels")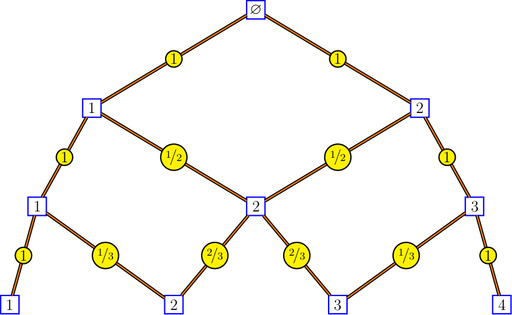

The intrinsic kernels are returned by the function bratteliKernels. The intrinsic distances between two vertices at the same level are returned by the function bratteliDistances.

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.