The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

bases

bases provides various basis expansions for flexible regression modeling, including random Fourier features (?b_rff), exact kernel / Gaussian process feature maps (?b_ker), Bayesian Additive Regression Trees prior features (?b_bart), and a helpful interface for n-way interactions (?b_inter). The provided functions may be used within any modeling formula, allowing the use of kernel methods and other basis expansions in modeling functions that do not otherwise support them.

Along with the basis expansions, a number of kernel functions (?kernels) are also provided, which support kernel arithmetic to form new kernels. Basic ridge regression functionality (?ridge) is included as well.

Finally, the package provides a recipes-friendly interface, so that these basis expansions can be combined with other transformations and used within the tidymodels framework.

Installation

You can install bases from CRAN:

install.packages("bases")

You can install the development version with

remotes::install_github("CoryMcCartan/bases")

Example: random Fourier features

The basis functions in bases all start with b_ and are designed to work in the same way as built-in basis expansions like bs() or poly(): simply include the function in a model formula.

So fitting an approximate kernel regression with random Fourier features is as simple as wrapping the relevant variables in a call to the corresponding basis function, b_rff(). The default kernel is a Gaussian/RBF kernel with length scale 1 which is applied to predictors after rescaling them to have unit variance.

library(bases)

# Box & Jenkins (1976) sales data
x = 1:150
y = as.numeric(BJsales) 

lm(y ~ b_rff(x, p = 5)) # 5 random features
#> 
#> Call:
#> lm(formula = y ~ b_rff(x, p = 5))
#> 
#> Coefficients:
#>      (Intercept)  b_rff(x, p = 5)1  b_rff(x, p = 5)2  b_rff(x, p = 5)3  
#>         -1821607             12882             33383            -35639  
#> b_rff(x, p = 5)4  b_rff(x, p = 5)5  
#>            88853           4123981

You can provide a different kernel = argument to switch kernels. Many common kernels are provided with the package; see ?kernels.

b_rff(x, kernel = k_matern(scale = 0.1, nu = 5/2))
b_rff(x, kernel = k_rq(scale = 2, alpha = 2))

In practice, RFF are usually fit with penalization, such as via ridge regression. Below, we visualize several RFF ridge regression fits versus a simple linear model, using the ridge() function provided in the package.

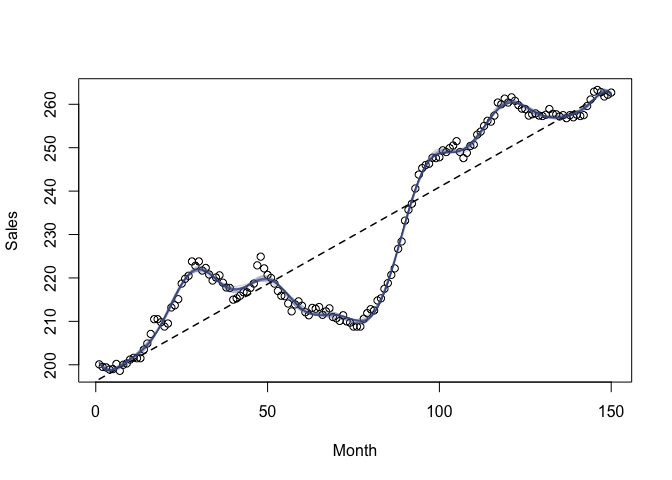
k = k_rbf(scale = 0.2)
plot(x, y, xlab = "Month", ylab = "Sales")
lines(x, fitted(lm(y ~ x)), lty = "dashed", lwd = 1.5)
for (i in 1:20) {
    m_rff = ridge(y ~ b_rff(x, kernel = k))
    lines(x, fitted(m_rff), col = "#4584")
}

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.