The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

alkahest

Overview

alkahest is a lightweight, dependency-free toolbox for pre-processing XY data from experimental methods (i.e. any signal that can be measured along a continuous variable). It provides methods for baseline estimation and correction, smoothing, normalization, integration and peaks detection.

To cite alkahest in publications use:

  Frerebeau N (2023). _alkahest: Pre-Processing XY Data from
  Experimental Methods_. Université Bordeaux Montaigne, Pessac, France.
  doi:10.5281/zenodo.7081524 <https://doi.org/10.5281/zenodo.7081524>,
  R package version 1.1.1, <https://packages.tesselle.org/alkahest/>.

Une entrée BibTeX pour les utilisateurs LaTeX est

  @Manual{,
    author = {Nicolas Frerebeau},
    title = {{alkahest: Pre-Processing XY Data from Experimental Methods}},
    year = {2023},
    organization = {Université Bordeaux Montaigne},
    address = {Pessac, France},
    note = {R package version 1.1.1},
    url = {https://packages.tesselle.org/alkahest/},
    doi = {10.5281/zenodo.7081524},
  }

This package is a part of the tesselle project
<https://www.tesselle.org>.

Installation

You can install the released version of alkahest from CRAN with:

install.packages("alkahest")

And the development version from GitHub with:

# install.packages("remotes")
remotes::install_github("tesselle/alkahest")

Usage

## Load the package
library(alkahest)

alkahest expects the input data to be in the simplest form (a two-column matrix or data frame, a two-element list or two numeric vectors).

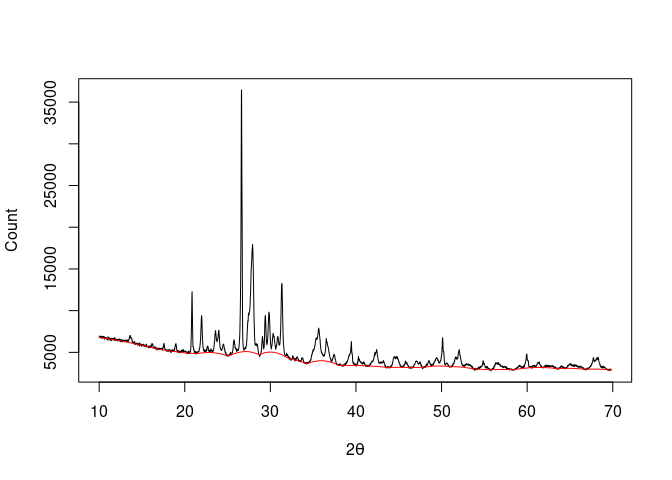
## X-ray diffraction
data("XRD")

## 4S Peak Filling baseline
baseline <- baseline_peakfilling(XRD, n = 10, m = 5, by = 10, sparse = TRUE)

plot(XRD, type = "l", xlab = expression(2*theta), ylab = "Count")
lines(baseline, type = "l", col = "red")

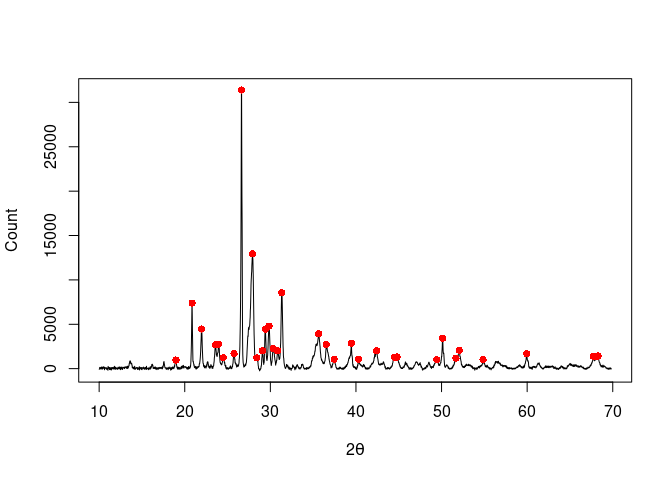
## Correct baseline
XRD <- signal_drift(XRD, lag = baseline, subtract = TRUE)

## Find peaks
peaks <- peaks_find(XRD, SNR = 3, m = 11)

plot(XRD, type = "l", xlab = expression(2*theta), ylab = "Count")
lines(peaks, type = "p", pch = 16, col = "red")

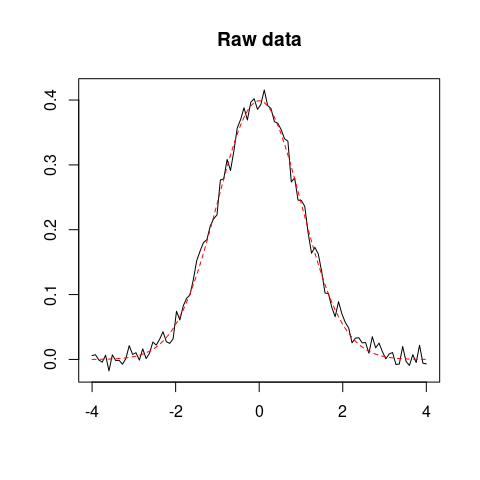
## Simulate data
set.seed(12345)
x <- seq(-4, 4, length = 100)
y <- dnorm(x)
z <- y + rnorm(100, mean = 0, sd = 0.01) # Add some noise

## Plot raw data
plot(x, z, type = "l", xlab = "", ylab = "", main = "Raw data")
lines(x, y, type = "l", lty = 2, col = "red")

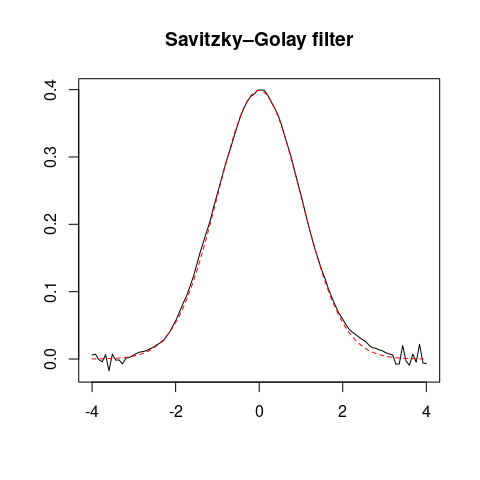
## Savitzky–Golay filter
smooth <- smooth_savitzky(x, z, m = 21, p = 2)
plot(smooth, type = "l", xlab = "", ylab = "", main = "Savitzky–Golay filter")
lines(x, y, type = "l", lty = 2, col = "red")

Contributing

Please note that the alkahest project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.