The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.
Alternating recurrent event data arise frequently in biomedical and social sciences where two types of events such as hospital admissions and discharges occur alternatively over time. BivRec implements a collection of nonparametric and semiparametric methods to analyze such data.
The main functions are:
- bivrecReg: Use for the estimation of covariate effects on the two
alternating event gap times (Xij and Yij) using semiparametric methods.
The method options are “Lee.et.al” and “Chang”.
- bivrecNP: Use for the estimation of the joint cumulative distribution
function (cdf) for the two alternating events gap times (Xij and Yij) as
well as the marginal survival function for type I gap times (Xij) and
the conditional cdf of the type II gap times (Yij) given an interval of
type I gap times (Xij) in a nonparametric fashion.
The package also provides options to simulate and visualize the data and results of analysis.
BivRec depends on the following system requirements:
- Rtools. Download Rtools 35 from https://cran.r-project.org/bin/windows/Rtools/
Once those requirements are met you can install BivRec from github as follows:
#Installation requires devtools package.
#install.packages("devtools")
library(devtools)
#install_github("SandraCastroPearson/BivRec")This is an example using a simulated data set.
# Simulate bivariate alternating recurrent event data
library(BivRec)
set.seed(28)
sim_data <- simBivRec(nsize=100, beta1=c(0.5,0.5), beta2=c(0,-0.5), tau_c=63, set=1.1)
head(sim_data)
#> id epi xij yij ci d1 d2 a1 a2
#> 1 1 1 5.396514 2.649410 11.76916 1 1 0 0.7455188
#> 2 1 2 3.723235 0.000000 11.76916 0 0 0 0.7455188
#> 3 2 1 5.648637 2.247070 45.31703 1 1 0 0.3344112
#> 4 2 2 2.949107 2.032798 45.31703 1 1 0 0.3344112
#> 5 2 3 4.437588 2.936018 45.31703 1 1 0 0.3344112
#> 6 2 4 3.114917 3.337000 45.31703 1 1 0 0.3344112
# Create a bivrecSurv object
bivrec_object <- with(sim_data, bivrecSurv(id, epi, xij, yij, d1, d2))
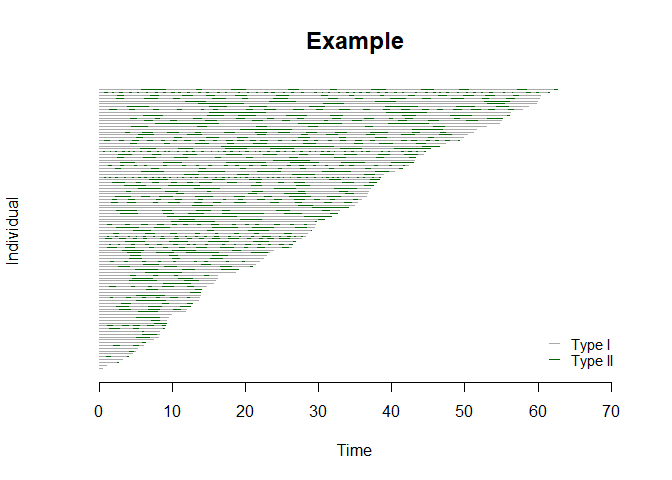
# Plot gap times
plot(bivrec_object, main="Example", type = c("Type I", "Type II"), col = c("darkgrey","darkgreen"))
Nonparametric Analysis
# Apply the nonparametric method of Huang and Wang (2005) and visualize joint, marginal and conditional results
library(BivRec)
npresult <- bivrecNP(response = with(sim_data, bivrecSurv(id, epi, xij, yij, d1, d2)),
ai=1, u1 = seq(1, 15, 0.5), u2 = seq(1, 15, 0.5), conditional = TRUE,
given.interval = c(1, 10), level = 0.99)
#> [1] "Estimating joint CDF and marginal survival"
#> [1] "Estimating conditional cdf with 99% confidence interval using 200 bootstrap samples"
head(npresult)
#>
#> Joint CDF:
#> x y Joint Probability SE Lower .99 Upper .99
#> 1 1 1.0 0.05900966 0.01967078 0.008341088 0.1096782
#> 2 1 1.5 0.06086021 0.01995590 0.009457207 0.1122632
#> 3 1 2.0 0.06179946 0.01994861 0.010415238 0.1131837
#> 4 1 2.5 0.06179946 0.01994861 0.010415238 0.1131837
#> 5 1 3.0 0.06179946 0.01994861 0.010415238 0.1131837
#> 6 1 3.5 0.06179946 0.01994861 0.010415238 0.1131837
#>
#> Marginal Survival:
#> Time Marginal Survival SE Lower .99 Upper .99
#> 1 0.3120105 0.9997561 0.0000243843 0.9996933 0.9998189
#> 2 0.3408594 0.9995122 0.0002438430 0.9988841 1.0000000
#> 3 0.3769168 0.9992683 0.0004858536 0.9980168 1.0000000
#> 4 0.3793933 0.9990302 0.0007282511 0.9971543 1.0000000
#> 5 0.3859942 0.9987863 0.0007635383 0.9968196 1.0000000
#> 6 0.3878224 0.9985424 0.0009969369 0.9959745 1.0000000
#>
#> Conditional CDF:
#> Time Conditional Probability Bootstrap SE Bootstrap Lower .99
#> 1 0.0000 0.0000 0.0000 0.00
#> 2 0.0776 0.0000 0.0000 0.00
#> 3 0.1551 0.0000 0.0000 0.00
#> 4 0.2327 0.0018 0.0011 0.00
#> 5 0.3103 0.0095 0.0038 0.00
#> 6 0.3878 0.0224 0.0081 0.01
#> Bootstrap Upper .99
#> 1 0.00
#> 2 0.00
#> 3 0.00
#> 4 0.00
#> 5 0.02
#> 6 0.04
plot(npresult)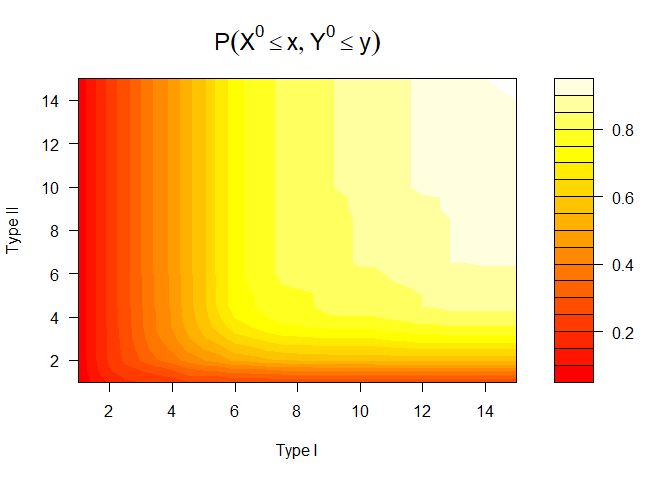
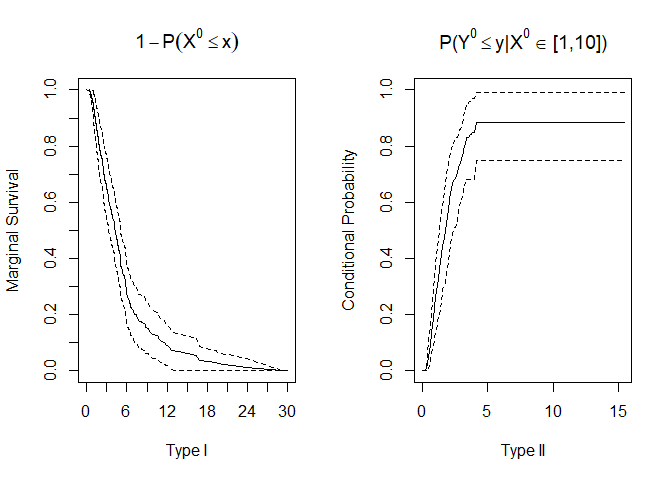
# To save individual plots in a pdf file un-comment the following line of code:
# pdf("nonparam_jointcdfplot.pdf")
# plotJoint(npresult)
# dev.off()
# pdf("nonparam_marginalplot.pdf")
# plotMarg(npresult)
# dev.off()
# pdf("nonparam_conditionaplot.pdf")
# plotCond(npresult)
# dev.off()Semiparametric Regression Analysis
#Explore how the response changes by levels of a categorical covariate using a plot.
#Use attach as follows or specifiy each vector using the $ operator (sim_data$id, sim_data$epi, etc.)
attach(sim_data)
plot(x = bivrecSurv(id, epi, xij, yij, d1, d2), by = data.frame(a1, a2),
type = c("Type I", "Type II"), col = c("darkgrey","darkgreen"))
#> [1] "a2 not used - either continuous or had more than 6 levels."
#> [1] "Subjects for plots: 100."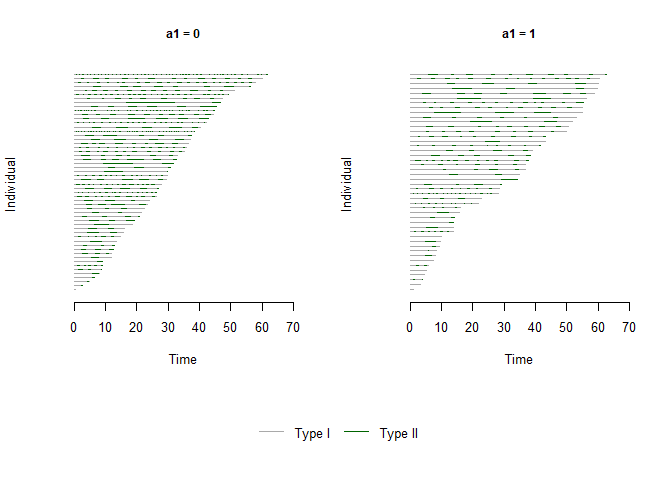
detach(sim_data)
# Apply Lee, Huang, Xu, Luo (2018) method using multiple covariates.
lee_fit <- bivrecReg(bivrecSurv(id, epi, xij, yij, d1, d2) ~ a1 + a2,
data= sim_data, "Lee.et.al")
#> [1] "Fitting model with covariates: a1, a2"
#> [1] "Estimating standard errors"
summary(lee_fit)
#>
#> Call:
#> bivrecReg(formula = bivrecSurv(id, epi, xij, yij, d1, d2) ~ a1 +
#> a2, data = sim_data, method = "Lee.et.al")
#>
#> Number of Subjects:
#> 100
#>
#> Coefficients:
#> Estimates SE z Pr(>|z|)
#> xij a1 0.686004 0.171881 3.9912 3e-05 ***
#> xij a2 0.293041 0.304425 0.9626 0.16787
#> yij a1 -0.057268 0.294032 -0.1948 0.42279
#> yij a2 -0.911427 0.480674 -1.8961 0.02897 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> exp(coefficients):
#> exp(coeff) Lower .95 Upper .95
#> xij a1 1.98576 1.41782 2.7812
#> xij a2 1.34050 0.73814 2.4344
#> yij a1 0.94434 0.53070 1.6804
#> yij a2 0.40195 0.15668 1.0312
# To apply Chang (2004) method use method="Chang".
# chang_fit <- bivrecReg(bivrecSurv(id, epi, xij, yij, d1, d2) ~ a1 + a2,
# data= sim_data, "Chang")These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.