The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

The BAS R
package is designed to provide an easy to use package and fast code for
implementing Bayesian Model Averaging and Model Selection in
R using state of the art prior distributions for linear and
generalized linear models. The prior distributions in BAS
are based on Zellner’s g-prior or mixtures of g-priors for linear and
generalized linear models. These have been shown to be consistent
asymptotically for model selection and inference and have a number of
computational advantages. BAS implements three main
algorithms for sampling from the space of potential models: a
deterministic algorithm for efficient enumeration, adaptive sampling
without replacement algorithm for modest problems, and a MCMC algorithm
that utilizes swapping to escape from local modes with standard
Metropolis-Hastings proposals.
The stable version can be installed
easily in the
R console like any other package:
install.packages('BAS')On the other hand, I welcome everyone to use the most recent version
of the package with quick-fixes, new features and probably new bugs.
It’s currently hosted on GitHub. To get the
latest development version from GitHub, use the
devtools package from CRAN and enter in
R:
devtools::install_github('merliseclyde/BAS')You can check out the current build status before installing.
Installing the package from source does require compilation of C and FORTRAN code as the library makes use of BLAS and LAPACK for efficient model fitting. See CRAN manuals for installing packages from source under different operating systems.
To begin load the package:
library(BAS)The two main function in BAS are bas.lm and
bas.glm for implementing Bayesian Model Averaging and
Variable Selection using Zellner’s g-prior and mixtures of g priors.
Both functions have a syntax similar to the lm and
glm functions respectively. We illustrate using
BAS on a simple example with the famous Hald data set using
the Zellner-Siow Cauchy prior via
data(Hald)
hald.ZS = bas.lm(Y ~ ., data=Hald, prior="ZS-null", modelprior=uniform(), method="BAS")BAS has summary, plot
coef, predict and fitted
functions like the lm/glm functions. Images of
the model space highlighting which variable are important may be
obtained via
image(hald.ZS)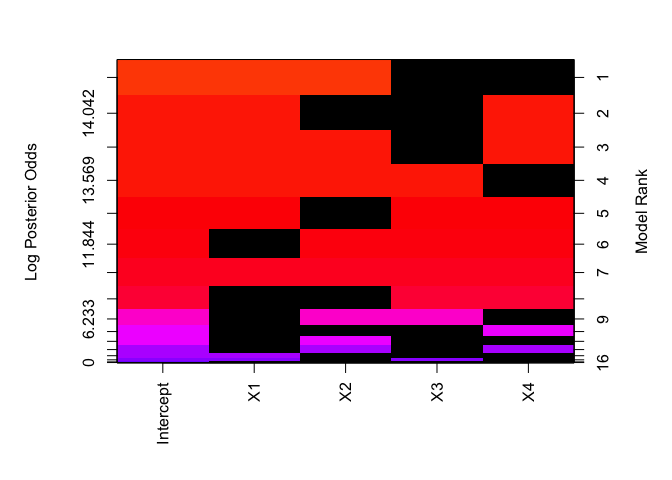
Run demo("BAS.hald") or demo("BAS.USCrime")
or see the package vignette for more examples and options such as using
MCMC for model spaces that cannot be enumerated.
BAS now includes for support for binomial and binary
regression, Poisson regression, and Gamma regression using Laplace
approximations to obtain Bayes Factors used in calculating posterior
probabilities of models or sampling of models. Here is an example using
the Pima diabetes data set with the hyper-g/n prior:
library(MASS)
data(Pima.tr)
Pima.hgn = bas.glm(type ~ ., data=Pima.tr, method="BAS", family=binomial(),
betaprior=hyper.g.n(), modelprior=uniform())Note, the syntax for specifying priors on the coefficients in
bas.glm uses a function with arguments to specify the
hyper-parameters, rather than a text string to specify the prior name
and a separate argument for the hyper-parameters. bas.lm
will be moving to this format sometime in the future.
Feel free to report any issues or request features to be added via the github issues page.
For current documentation and vignettes see the BAS website
This material is based upon work supported by the National Science Foundation under Grant DMS-1106891. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.