The hardware and bandwidth for this mirror is donated by dogado GmbH, the Webhosting and Full Service-Cloud Provider. Check out our Wordpress Tutorial.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]dogado.de.

tidydice

Simulates Dice Rolls and Coin Flips.

Introduction

A basic understanding of probability and statistics is crucial for data understanding. A great way to teach probability and statistics is to start with an experiment, like rolling a dice or flipping a coin.

This package simulates rolling a dice and flipping a coin. Each experiment generates a tibble. Dice rolls and coin flips are simulated using sample(). The properties of the dice can be changed, like the number of sides. A coin flip is simulated using a two sided dice. Experiments can be combined with the pipe-operator.

Installation

CRAN

install.packages("tidydice")

DEV version (github)

# install from github
if (!require(devtools)) install.packages("devtools")
devtools::install_github("rolkra/tidydice")

if you are behind a firewall, you may want to:

• Download and unzip the tidydice package
• Then install it with devtools::install_local

# install local
if (!require(devtools)) install.packages("devtools")
devtools::install_local(path = <path of local package>, force = TRUE)

Basic example

Let’s roll 60 dice:

# load packages
library(tidydice)

# roll 60 dice (10 x 6 dice = 60)
data <- roll_dice(times = 10, rounds = 6)
data

We get tidy data, where each row is a dice. It is a success, if the result is a 6.

# A tibble: 60 × 5
   experiment round    nr result success
        <int> <int> <int>  <int> <lgl>  
 1          1     1     1      5 FALSE  
 2          1     1     2      6 TRUE   
 3          1     1     3      6 TRUE   
 4          1     1     4      1 FALSE  
 5          1     1     5      5 FALSE  
 6          1     1     6      1 FALSE  
 7          1     1     7      4 FALSE  
 8          1     1     8      5 FALSE  
 9          1     1     9      1 FALSE  
10          1     1    10      2 FALSE  
# … with 50 more rows

Now let’s plot it:

data |> plot_dice()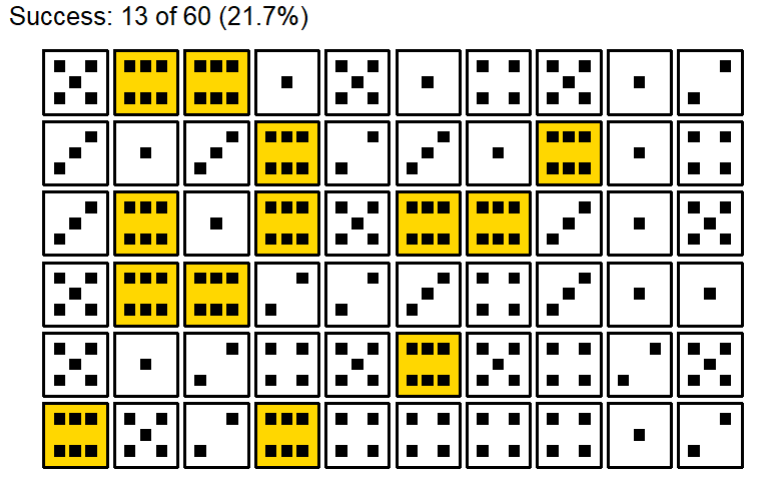

We got 13 six. Is this unlikely? The expected value is 10 (60 dice / 6 sides = 10). So 13 is more than expected, is it a sign of cheating? Let’s check using the binomial ditribution:

# binomial distribution
binom_dice(times = 60) |> 
  plot_binom(highlight = c(13:60))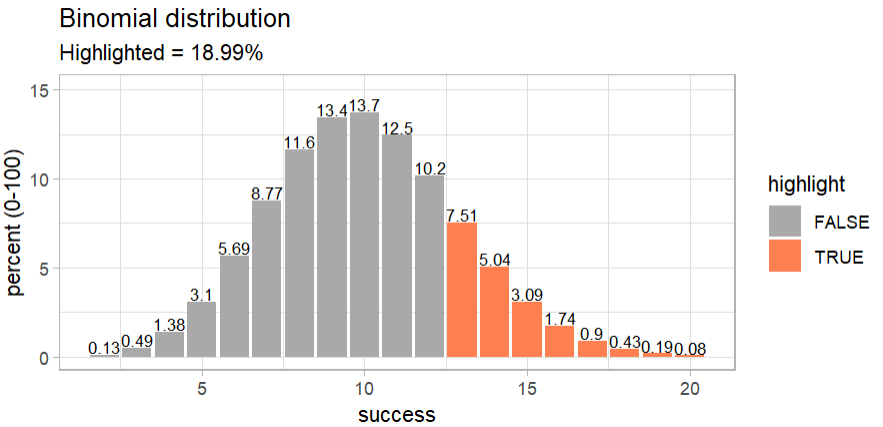

The binomial distribution shows, that there is a 19% chance that you can get 13 or more six using a fair dice.

Roll dice

# load packages
library(tidydice)

# roll a dice
roll_dice()

# roll a dice 6x
roll_dice(times = 6)

# roll a dice 6x and plot result
roll_dice(times = 6) |> 
  plot_dice()

# repeat 6x
roll_dice(times = 6, rounds = 6)  |>  
  plot_dice()

# count success per round
roll_dice(times = 6, rounds = 6, agg = TRUE)

# Binomial distribution
binom_dice(times = 6)
  
# Binomial distribution + plot
binom_dice(times = 6) |>  
  plot_binom()

# Binomial distribution + plot 
binom_dice(times = 6) |>  
  plot_binom(highlight = 0:2)

Roll dice (advanced)

To do more complex dice rolls use roll_dice_formula():

library(tidydice)

roll_dice_formula(
  dice_formula = "4d6e3", # 4 dice with 6 sides, explode on a 3
  rounds = 5,             # repeat 5 times
  success = 15:24,        # success is defined as sum between 15 and 24
  seed = 123              # random seed to make it reproducible
)

• 1d6 = roll one 6-sided dice
• 1d8 = roll one 8-sided dice
• 1d12 = roll one 12-sided dice
• 2d6 = roll two 6-sided dice
• 1d6e6 = roll one 6-sided dice, explode dice on a 6
• 3d6kh2 = roll three 6-sided dice, keep highest 2 rolls
• 3d6kl2 = roll three 6-sided dice, keep lowest 2 rolls
• 4d6kh3e6 = roll four 6-sided dice, keep highest 3 rolls, but explode on a 6
• 1d20+4 = roll one 20-sided dice, and add 4
• 1d4+1d6 = roll one 4-sided dice and one 6-sided dice, and sum the results

Flip coin

# load packages
library(tidydice)

# flip a coin
flip_coin()

# flip a coin 10x
flip_coin(times = 10)

# flip a coin 10x and plot result
flip_coin(times = 10) |> 
  plot_coin()

# repeat 10x and plot result
flip_coin(times = 10, rounds = 10) |> 
  plot_coin()

# count success per round
flip_coin(times = 10, rounds = 10, agg = TRUE)

# Binomial distribution
binom_coin(times = 10)
  
# Binomial distribution + plot
binom_coin(times = 10) |>  
  plot_binom()

# Binomial distribution + plot 
binom_coin(times = 10) |>  
  plot_binom(highlight = 0:2)

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.
Health stats visible at Monitor.